








La dérivée est une notion clef dans l’analyse de fonctions, car elle sous-tend toute la science physique.
Soit une fonction \( f :x \longmapsto f(x) \) continue sur son ensemble de définition.
On appelle \( f'(a) \) le nombre dérivé de la fonction \( f \) au point \( (x=a )\) tel que :
$$ f'(a) = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$
Si (et seulement si) ce nombre existe, on dit alors que \( f \) est dérivable en un point \(a\).
$$ f \ dérivable \ en \ a \Longleftrightarrow lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
En déterminant l'expression générale de la fonction dérivée \(f'\), on pourra définir où est-ce que la fonction \(f\) est dérivable.
La fonction \(f'\), dérivée de la \( f \) s'exprime ainsi :
$$ f'(x) = lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$
C'est la limite du taux de variation quand \( h \to 0 \).
On pourra aussi la retrouver sous cette forme :
$$ f'(x) = lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$
À ce moment-là, ce sera la limite du taux de variation quand \( x \to a \).
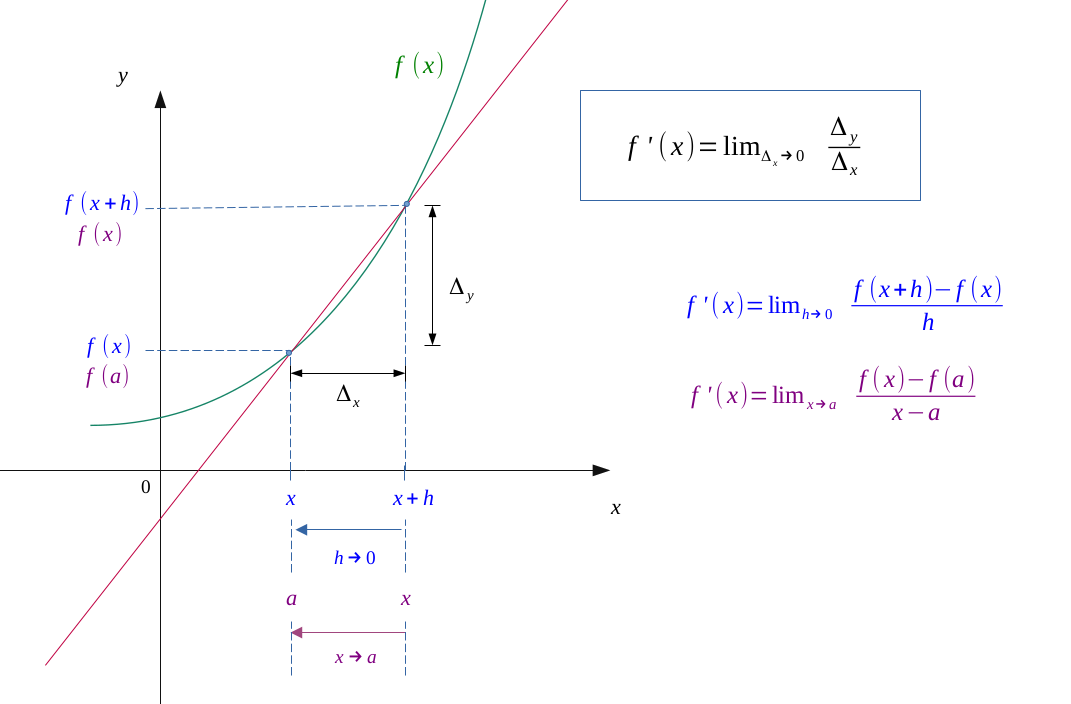
La dérivabilité implique la continuité
$$ f \ dérivable \ en \ a \Longrightarrow f \ continue \ en \ a $$
Le signe de la dérivée indique le sens de variation
$$ \forall x \in [a,b], \ f'(x) \geqslant 0 \ \Longleftrightarrow f \ croissante \ sur \ [a,b] $$
$$ \forall x \in [a,b], \ f'(x) \leqslant 0 \ \Longleftrightarrow f \ décroissante \ sur \ [a,b] $$
Équation de la tangente au point a
Nous avons dans la définition de la dérivée que le nombre dérivé correspondait à la pente de la tangente à la courbe d'une fonction.
Cette droite admet pour équation au point d'abscisse \((x = a)\) :
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
De plus, dans le cas d'une fonction convexe (resp. concave), cette tangente se situe toujours au dessous (resp. au dessus) de la courbe.
$$f \enspace convexe \enspace sur \enspace [a,b] \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a) $$
$$f \enspace concave \enspace sur \enspace [a,b] \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a)$$
Lien entre développement limité d'ordre 1 et dérivabilité
$$ f \ d\textit{é}rivable \ en \ a \ \Longleftrightarrow \ f \ admet \ un \ d\textit{é}veloppement \ limit\textit{é} \ d'ordre \ 1 \ en \ a$$
Soit une fonction \( f :x \longmapsto f(x) \), continue sur un intervalle \( [a, \ a+h] \).
Nous y situons deux points sur l’axe des abscisses, \( a \) et \( a +h \) (\( h \) étant une distance relativement petite). Leur image étant respectivement \( f(a) \) et \( f(a + h) \), on obtient deux points : \( A(a; f(a)) \) et \( B(a + h; f(a + h)) \).
On a de même tracé la droite qui les relie telle que la figure suivante :
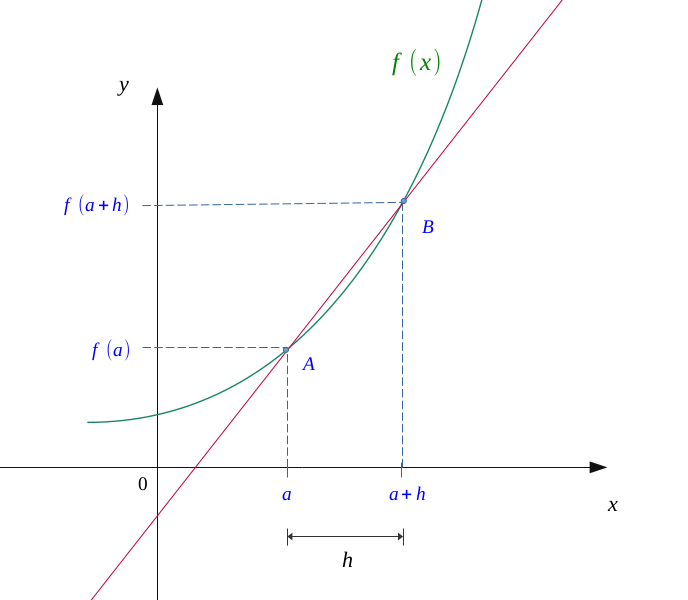
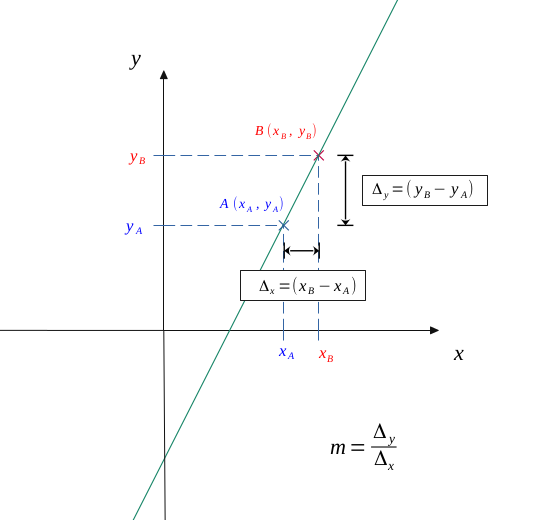
On peut alors calculer une pente moyenne de la variation de cette fonction entre \( A \) et \( B \).
Cette pente, nous pouvons la calculer avec la formule suivante :
$$ m = \frac{ \Delta _y}{\Delta _x}$$
$$ m = \frac{ y_B- y_A}{x_B- x_A}$$
Dans notre cas, cela donne :
$$ m = \frac{f(a+h) - f(a)}{ a + h -a} $$
Soit :
$$ m = \frac{f(a+h) - f(a)}{h} \qquad (1) $$
Nous allons alors réduire petit à petit cette distance \( h \) qui sépare nos deux points sur l’axe des abscisses, en faisant tendre progressivement le point \(B\) vers le point \(A\).
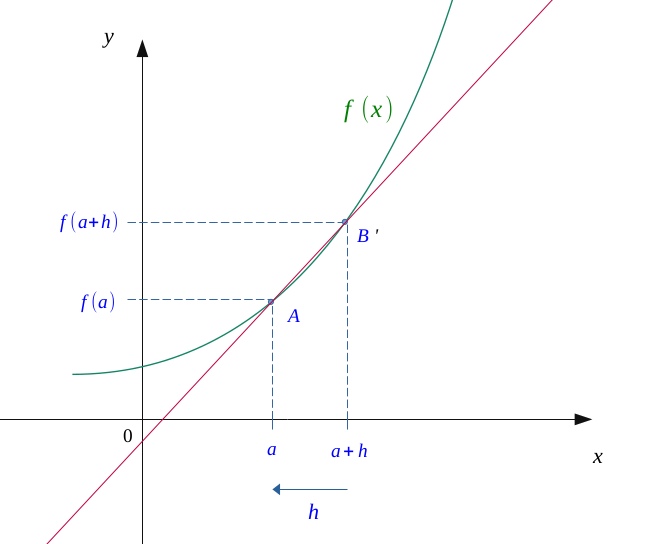
Nous voyons que les valeurs de \( a \) et \( (a + h) \) commencent à se rapprocher, et la droite qui relie les points \( A \) et \( B \) commencent à dessiner une tangente à la courbe.
De la même manière, nous allons encore réduire la distance \( h \), celle-ci commence à tendre vers \( 0 \).
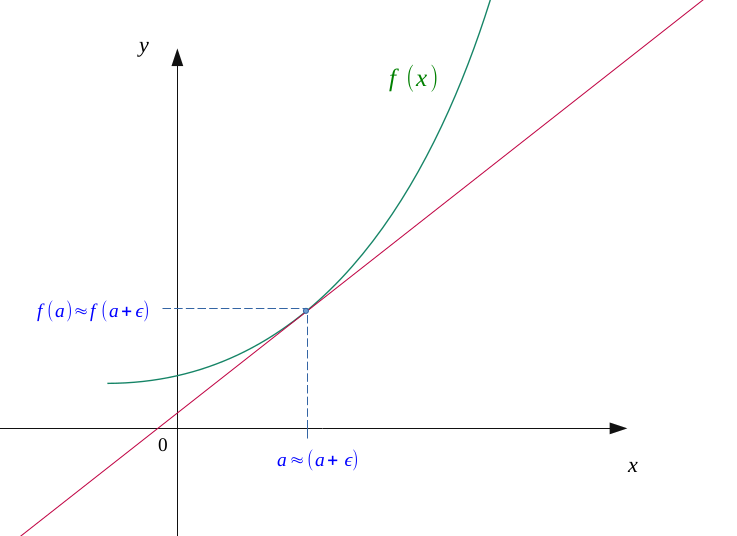
On voit à présent que les deux points \( A \) et \( B \) sont quasiment confondus, et que nous obtenons alors une tangente quasi-parfaite à la courbe au point d'abscisse \( a \).
En imaginant que \( h \) devient de plus en plus petit et s’approche de \( 0 \), notre formule \( (1) \) peut s'exprimer sous forme de limite :
$$ m = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h} $$
Ce nombre \( m\) obtenu, pour un \( a \) choisi arbitrairement, sera appelé le nombre dérivé de la fonction \( f \) au point \( a \). Il sera noté \( f'(a) \).
$$ f'(a) = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$
Si ce nombre n'est pas calculable, la dérivée n'est pas définie en ce point \( a \).
Maintenant, si (et seulement si) ce nombre existe, on dit alors que \( f \) est dérivable en un point \(a\).
$$ f \ dérivable \ en \ a \Longleftrightarrow lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
En déterminant l'expression générale de la fonction dérivée \(f'\), on pourra définir où est-ce que la fonction \(f\) est dérivable.
Et par généralisation, c'est-à-dire pour tout \( x \), on appelle \( f' \) la fonction dérivée de la fonction \( f \).
$$ f'(x) = lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$
L'ensemble de définition de \( f' \) dépendra alors de son expression, et sera restreint au maximum l'ensemble de définition de la fonction \( f \).
Par exemple, la fonction \( ln(x) \) n'est définie que sur \(\mathbb{R^*_+}\).
Alors, sa dérivée :
$$ ln(x)' = \frac{1}{x} $$
est elle aussi restreinte (a minima) à cet intervalle de départ, tandis que la fonction \( f: x \longmapsto \frac{1}{x} \) est normalement définie sur \(\mathbb{R^*}\), qui est un intervalle plus large.
On dit que la dérivée est la limite du taux de variation quand \( h \) tend vers \( 0 \).
On pourra aussi la retrouver sous cette forme :
$$ f'(x) = lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$
À ce moment-là, ce sera la limite du taux de variation quand \( x \to a \).

En physique, on pourra aussi utiliser la notation différentielle de Leibniz \( \frac{df}{dx} \), ou celle de Newton \( \overset{.}{f} \).
Particulièrement pour le calcul intégral, il est pratique d'utiliser celle de Leibniz.
On a vu que si une fonction est dérivable en un point \( a\), alors :
$$ lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
Par suite,
$$ lim_{h \to 0} \ f(a+h) = hf'(a) + f(a) $$
$$ lim_{h \to 0} \ f(a+h) = f(a)$$
Ce qui implique la continuité de la fonction \( f \) au point \( x = a\).
$$ f \ dérivable \ en \ a \Longrightarrow f \ continue \ en \ a $$
Soit une fonction \(f\) continue et positive sur \([a,b]\), et dérivable sur \( \hspace{0.1em} ]a,b[\).
De même, soient \( (x_1, x_2) \in \hspace{0.1em} ]a,b[ \), deux points intérieurs à \( \hspace{0.1em} ]a,b[\) dans cet ordre.
D'après le théorème des accroissements finis :
$$ f \ continue \ sur \ [a,b] \ et \ dérivable \ sur \ ]a,b[ \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a}$$
Dans notre cas,
$$ \forall (x_1, x_2) \in \hspace{0.1em} ]a,b[ ,$$
$$ \exists x_3 \in \hspace{0.05em} ]x_1, x_2[, \ f'(x_3) = \frac{ f(x_2) - f(x_1)}{x_2-x_1}$$
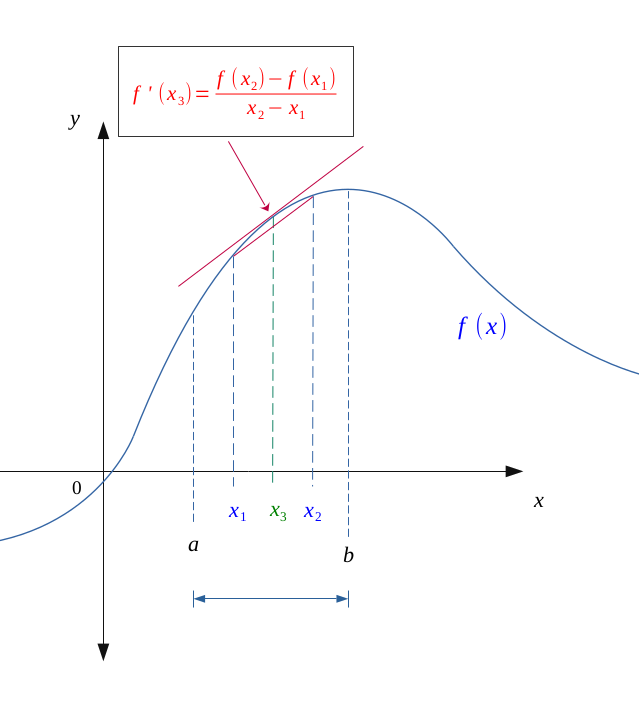
L'intervalle \((x_2-x_1)\) étant toujours positif, si la fonction \(f\) est croissante sur \([a,b]\), elle l'est donc aussi sur \(]x_1, x_2[\), et dans ce cas :
$$ f(x_2) - f(x_1) \geqslant 0 \Longleftrightarrow f'(x_3) \geqslant 0 $$
La dérivée \(f'\) de la fonction \(f\) sera alors positive pour tout \( x \in [a,b]\).
Le même raisonnement s'applique pour une fonction décroissante.
$$ \forall x \in [a,b], \ f'(x) \geqslant 0 \ \Longleftrightarrow f \ croissante \ sur \ [a,b] $$
$$ \forall x \in [a,b], \ f'(x) \leqslant 0 \ \Longleftrightarrow f \ décroissante \ sur \ [a,b] $$
Représentons un schéma d'une fonction et de sa tangente, issu du nombre dérivé au point d'abscisse \(a\).
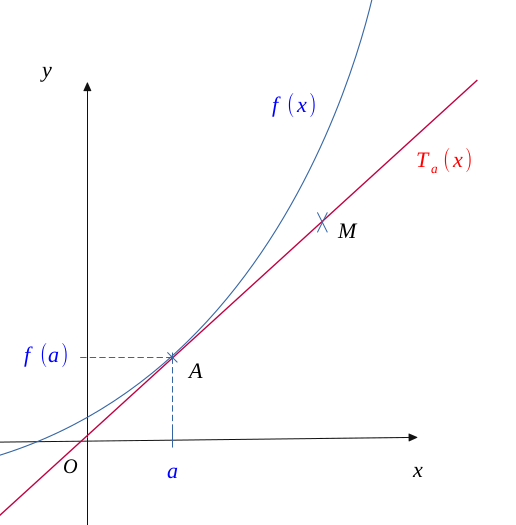
Le point \(a\) a alors pour image \( f(a)\) ou \( T_a(a)\) puisque par définition, une tangente est un point d'intersection.
On a de même placé un point théorique \( M(x, T_a(x))\) sur la tangente à la courbe.
En appliquant le calcul de la pente pour les points \( A \) et \( B \), on a :
$$ m = \frac{ \Delta y}{\Delta x}$$
$$ m = \frac{ T_a(x) - T_a(a)}{x - a} \qquad (2) $$
Or, on sait que la pente de la tangente à la courbe au point d'abscisse \( a \) est la même chose que le nombre dérivé en \( a \):
$$ m = f'(a) \qquad (3) $$
Soit, en injectant \( 3) \) dans \( (2) \),
$$ f'(a) = \frac{ T_a(x) - T_a(a)}{x - a}$$
$$ f'(a)(x - a) = T_a(x) - T_a(a) $$
Et comme \( T_a(a) = f(a) \),
$$ f'(a)(x - a) = T_a(x) - f(a) $$
La tangente à la courbe au point d'abscisse \(a\) admet pour équation :
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
Par ailleurs, dans le cas d'une fonction convexe, au sein d'un intervalle \(I = [a, b]\), toute corde allant de part et d'autre de ces deux points se situe au-dessus de la courbe.
Sa tangente ne peut alors qu'être au-dessous :
$$ f(x) \geqslant T_{a}(x) $$
$$f \enspace convexe \enspace sur \enspace [a,b] \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a) $$
$$f \enspace concave \enspace sur \enspace [a,b] \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a)$$
Et l'inégalité sera inversée dans le cas d'une fonction concave.
On a vu plus haut que l'équation de la tangente en un point \(a\) valait :
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
Alors, on peut représenter la courbe de cette tangente \(T_a\), avec celle de la fonction d'étude \(f\), et remarquer que pour tout point quelconque \(M(x, y)\), il existe une différence \(\varepsilon_a(x)\) entre ces deux fonctions.
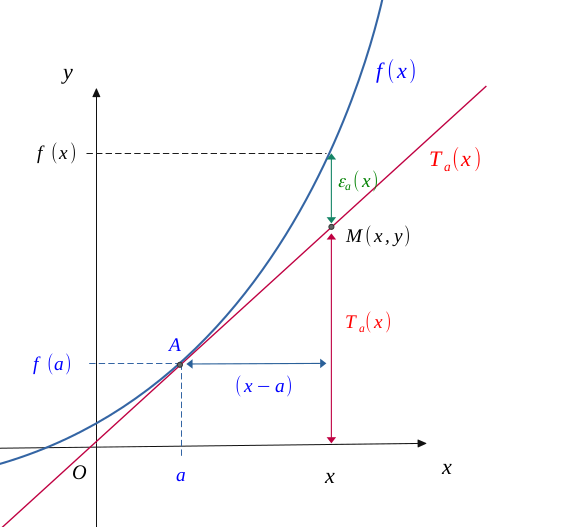
Si une fonction \(f\) admet un développement limité à l'ordre \(1\) en \(a\) \((DL_n(a))\), alors au voisinage de \((x = a) \) :
$$ f(x) = f(a) + f'(a)(x-a) + o(x-a) $$
$$ \Bigl( o\textit{ù} \enspace o(x-a) = (x-a) \varepsilon(x) \qquad \bigl(avec \enspace lim_{x \to a} \ \varepsilon(x) = 0 \bigr) \Bigr) $$
Ce qui implique l'existence de \(f'(a)\). Alors,
$$ f \ admet \ un \ d\textit{é}veloppement \ limit\textit{é} \ d'ordre \ 1 \ en \ a \ \Longrightarrow \ f \ d\textit{é}rivable \ en \ a$$
Si maintenant la fonction est dérivable en \(a\), alors comme l'illustre bien la figure précédente :
$$ \frac{f(x) - f(a)}{x-a} = \frac{T_a(x) + \varepsilon_a(x) - f(a) }{x-a} $$
En remplaçant \(T_a(x)\) par sa valeur, on obtient :
$$ \frac{f(x) - f(a)}{x-a} = \frac{f'(a)(x - a) + f(a) + \varepsilon_a(x) - f(a)}{x-a} $$
$$ f(x) - f(a) = f'(a)(x - a) + \varepsilon_a(x)(x-a) $$
Et finalement,
$$ f(x) = f(a) + f'(a)(x - a) + \varepsilon_a(x)(x-a) $$
Ce qui est la définition d'un développement limité à l'ordre \(1\). Alors,
$$ f \ d\textit{é}rivable \ en \ a \ \Longrightarrow \ f \ admet \ un \ d\textit{é}veloppement \ limit\textit{é} \ d'ordre \ 1 \ en \ a$$
Les deux implications précédentes donnent lieu à une équivalence, soit :
$$ f \ d\textit{é}rivable \ en \ a \ \Longleftrightarrow \ f \ admet \ un \ d\textit{é}veloppement \ limit\textit{é} \ d'ordre \ 1 \ en \ a$$
Étudions les variations de la fonction \(f\) suivante :
$$f(x) = \frac{1}{x} - 2\sqrt{x} $$
Cette fonction est uniquement définie sur : \( D_f = \ ] 0, +\infty[\).
On calcule sa dérivée \(f'\).
$$f(x) = \hspace{0.1em} \underbrace{-\frac{1}{x^2}} _\text{ \( < \hspace{0.2em} 0\)} - \hspace{0.1em} \underbrace{\frac{1}{\sqrt{x}} } _\text{ \( < \hspace{0.2em} 0\)} $$
\(f'(x)\) est toujours négative sur \(D_f\).
Alors, \(f(x)\) sera décroissante dans cette intervalle.
|
$$ x $$ |
$$ 0 $$ |
$$ \dots $$ |
$$ +\infty $$ |
|---|---|---|---|
|
$$ signe \ de \ f' $$ |
$$ \bigl ]-\infty \bigr] $$ |
$$- $$ |
$$ \bigl [ 0^- \bigr] $$ |
|
$$ variations \ de \ f $$ |
$$ \bigl [+\infty\bigr] $$ |
$$ \searrow $$ |
$$ \bigl ]-\infty \bigr] $$ |
Par ailleurs on a :
$$ \Biggl \{ \begin{align*} lim_{x \to 0} \ f(x) = +\infty \\ lim_{x \to +\infty} \ f(x) = -\infty \end{align*} $$
$$ \Biggl \{ \begin{align*} lim_{x \to 0} \ f'(x) = -\infty \\ lim_{x \to +\infty} \ f'(x) = \hspace{0.1em} 0^- \end{align*} $$
 Retour en haut de page
Retour en haut de page