








Soit deux fonctions \(f, g\) de classe \(\mathcal{C}^1\) sur un intervalle \(I = [a,b]\), et une fonction \(F\) primitive de \(f\).
L'intégrale de \(a\) vers \(b\) est l'aire située entre l'axe des abscisses la courbe de \(f\), entre les points \(a\) et \(b\) (voir lien entre intégrales et primitives).
Fonction définie par une intégrale
$$ \forall (a, x) \in D_f^2, $$
$$ F(x) = \int_{a}^x f(t) \hspace{0.2em}dt \Longrightarrow F(a) = 0$$
$$ \forall a \in D_f, $$
$$ \int_{a}^a f(t) \hspace{0.2em}dt =0 $$
$$ \forall (a,b) \in D_f^2, $$
$$ \int_{b}^a f(t) \hspace{0.2em}dt = -\int_{a}^b f(t) \hspace{0.2em}dt $$
$$ \forall (a, \lambda ,b) \in D_f^3, \enspace a \leqslant \lambda \leqslant b, $$
$$ \int_{a}^{\lambda} f(t) \hspace{0.2em}dt + \int_{\lambda}^b f(t) \hspace{0.2em}dt = \int_{a}^b f(t) \hspace{0.2em}dt $$
$$ \forall (a,b) \in D_f^2, \enspace \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \lambda \int_{a}^b f(t) \hspace{0.2em}dt + \mu \int_{a}^b g(t) \hspace{0.2em}dt $$
L'intégrale d'une combinaison linéaire de fonctions est la combinaison linéaire de l'intégrale de chaque fonction.
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ \enspace f(x) \geqslant 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \geqslant 0 $$
De la même manière, si \( f(x) \leqslant 0 \) sur \( [a, b] \),
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \textcolor{#A65757}{\leqslant} 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \textcolor{#A65757}{\leqslant} 0 $$
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \leqslant g(x) \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \leqslant \int_{a}^b g(t) \hspace{0.2em}dt $$
$$ \forall (a,b) \in D_f^2, $$
$$ \mu = \frac{1}{(b-a)} \int_{a}^b f(t) $$
$$ \forall (a,b) \in D_f^2, $$
$$ \exists c \in \hspace{0.05em} ]a,b[, \enspace f(c) = \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt$$
$$ \forall (a,b) \in D_f^2, \ \Bigl[ \forall x \in [a, b], \ m = min\{f\}, \ M = max\{f\} \Bigr], $$
$$ m \hspace{0.2em} \leqslant \hspace{0.2em} \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt \hspace{0.2em} \leqslant \hspace{0.2em} M $$
Récapitulatif des propriétés de l'intégrale
On sait par le lien entre intégrales et primitives que :
$$ F(x) = F(a) + \int_{a}^x f(t) \hspace{0.2em}dt $$
Or, si une fonction est définie par une intégrale, on a :
$$ F(x) = \int_{a}^x f(t) \hspace{0.2em}dt $$
Cela implique nécessairement que \( F(a) = 0 \).
Alors, \( F(x) \) est la primitive de \( f(x) \) qui s'annule en \( x = a \).
$$ \Biggl \{ \begin{gather*} F'(x) = f(x) \\ F(a) = 0 \end{gather*}$$
Soit finalement,
$$ \forall (a, x) \in D_f^2, $$
$$ F(x) = \int_{a}^x f(t) \hspace{0.2em}dt \Longrightarrow F(a) = 0$$
$$ ln(x) = \int_{1}^x \frac{dt}{t} $$
On sait par le lien entre intégrales et primitives que :
$$ F(x) = F(a) + \int_{a}^x f(t) \hspace{0.2em}dt $$
Soit que,
$$ \int_{a}^x f(t) \hspace{0.2em}dt = F(x) - F(a) $$
Si \( x = a \), alors :
$$ \int_{a}^a f(t) \hspace{0.2em}dt = F(a) - F(a) = 0 $$
La fonction \(F \) est la primitive de \(f\) qui s'annule au point \(x=a\).
Soit finalement,
$$ \forall a \in D_f, $$
$$ \int_{a}^a f(t) \hspace{0.2em}dt =0 $$
On sait par le lien entre intégrales et primitives que :
$$ F(x) = F(a) + \int_{a}^x f(t) \hspace{0.2em}dt $$
Soit que,
$$ \int_{a}^x f(t) \hspace{0.2em}dt = F(x) - F(a) $$
En inversant le sens des bornes, on a :
$$ \int_{a}^x f(t) \hspace{0.2em}dt = F(a) - F(x) = -(F(x) - F(a)) $$
$$ \int_{x}^a f(t) \hspace{0.2em}dt = - \int_{a}^x f(t) \hspace{0.2em}dt $$
Soit finalement,
$$ \forall (a,b) \in D_f^2, $$
$$ \int_{b}^a f(t) \hspace{0.2em}dt = -\int_{a}^b f(t) \hspace{0.2em}dt $$
On sait par le lien entre intégrales et primitives que :
$$ F(x) = F(a) + \int_{a}^x f(t) \hspace{0.2em}dt $$
Soit que,
$$ \int_{a}^x f(t) \hspace{0.2em}dt = F(x) - F(a) $$
D'où,
$$ \int_{a}^b f(t) \hspace{0.2em}dt + \int_{b}^c f(t) \hspace{0.2em}dt = F(b) - F(a) + F(c) - F(b) $$
$$ \int_{a}^b f(t) \hspace{0.2em}dt + \int_{b}^c f(t) \hspace{0.2em}dt = F(c) - F(a) $$
Soit finalement,
$$ \forall (a, \lambda ,b) \in D_f^3, \enspace a \leqslant \lambda \leqslant b, $$
$$ \int_{a}^{\lambda} f(t) \hspace{0.2em}dt + \int_{\lambda}^b f(t) \hspace{0.2em}dt = \int_{a}^b f(t) \hspace{0.2em}dt $$
Soit deux fonctions \(f,g\) continues sur \(I = [a,b]\), et deux fonctions \(F,G\) une de leurs primitives respectives.
De même, soit deux réels \( (\lambda , \mu) \in \hspace{0.05em} \mathbb{R}^2 \) qui nous permettent de construire une nouvelle fonction \(\Lambda\), combinaison linéaire de \(f\) et de \(g\) :
$$ \Lambda = \lambda f(t) + \mu g(t) $$
En intégrant cette fonction entre les bornes \(a\) et \(b\), on a :
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \Biggl[\lambda F(t) + \mu G(t) \Biggr]_a^b $$
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \lambda F(b) - \lambda F(a) + \mu G(b) - \mu G(a) $$
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \lambda \bigl(F(b) - F(a)\bigl) \hspace{0.1em} + \hspace{0.1em} \mu \bigl(G(b) - G(a)\bigl) $$
Mais,
$$\left\{ \begin{gather*} F(b) - F(a) = \int_{a}^b f(t) \\ G(b) - G(a) = \int_{a}^b g(t) \end{gather*} \right\}$$
Soit finalement,
$$ \forall (a,b) \in D_f^2, \enspace \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ \int_{a}^b \biggl(\lambda f(t) + \mu g(t) \hspace{0.2em} \biggr) dt = \lambda \int_{a}^b f(t) \hspace{0.2em}dt + \mu \int_{a}^b g(t) \hspace{0.2em}dt $$
L'intégrale d'une combinaison linéaire de fonctions est la combinaison linéaire de l'intégrale de chaque fonction.
Soit une fonction \(f\) continue sur \(I = [a,b]\) et pour tout \( x \in I, \enspace f(x) \geqslant 0\).
Si une fonction \(F\) est une primitive de \(f\) sur \(I\), alors :
$$ \forall x \in I, \enspace F(x) = F(a) + \int^x f(t) \hspace{0.2em}dt $$
$$ F'(x) = \hspace{0.2em} \underbrace {(F(a))'} _\text{= 0} \hspace{0.2em} + \hspace{0.2em} f(x) $$
Soit que,
$$ F'(x) = f(x) $$
Comme on a comme hypothèse que \( f(x) \geqslant 0\), alors \( F'(x) \geqslant 0\).
Cela implique que \( F(x)\) est croissante sur \( I\).
$$ \Biggl \{ \begin{gather*} f(x) \geqslant 0 \\ F'(x) = f(x) \end{gather*} \hspace{0.2em} \Longrightarrow \hspace{0.2em} F'(x) \geqslant 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} F \nearrow $$
Et dans ce cas, on a :
$$ F(a) \leqslant F(b) \hspace{0.2em} \Longrightarrow \hspace{0.2em} F(b) - F(a) \geqslant 0 $$
Soit que,
$$ \int_{a}^b f(t) \hspace{0.2em}dt \geqslant 0 $$
Soit finalement,
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \geqslant 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \geqslant 0 $$
De la même manière, si \( f(x) \leqslant 0 \) sur \( [a, b] \),
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ f(x) \textcolor{#A65757}{\leqslant} 0 \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \textcolor{#A65757}{\leqslant} 0 $$
On sait que l'interprétation géométrique de l'intégrale d'une fonction entre deux bornes \(a\) et \(b\) est le fait qu'elle soit égale à l'aire entre la courbe de la fonction et l'axe des abscisses, tel que la figure suivante :
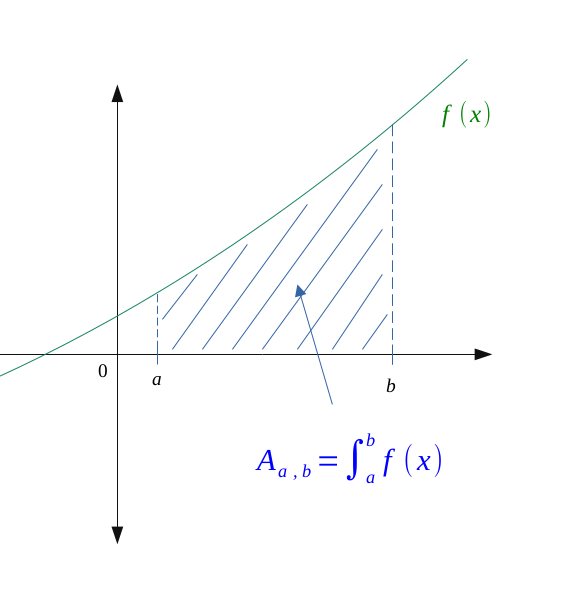
Mais grâce à la croissance de l'intégrale, le signe d'une intégrale va suivre le signe de la fonction intégrée sur l'intervalle d'étude. Donc dans le cas d'une fonction négative, on aura une intégrale négative.
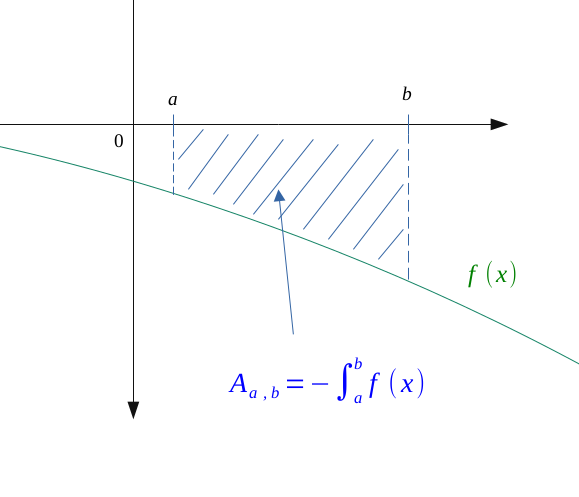
Par conséquent, si l'on veut calculer l'aire totale d'une fonction à la fois négative et positive sur son intervalle d'étude, il nous faut changer le signe de la partie négative pour obtenir une valeur positive.
Effectivement, une aire négative ne pourrait avoir de sens physique.
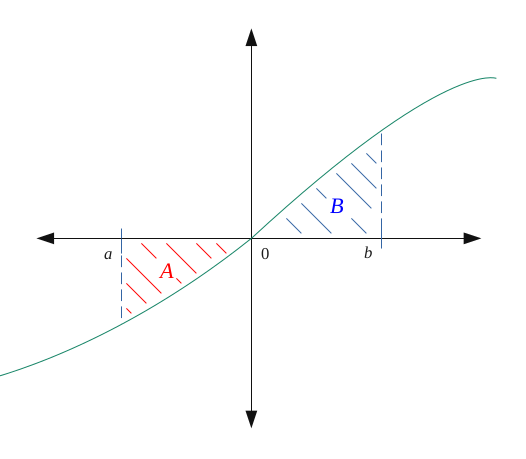
Appellons \(S\) la somme des surfaces \(A\) et \(B\).
$$ S = A + B $$
Pour obtenir \(S\), on doit inverser le signe de l'intégrale là où \(f(x) \leqslant 0\). Ici en l'occurrence pour \( x \in [a, 0]\).
$$ S = - \hspace{0.2em} \underbrace{\int_{a}^0 f(t) \hspace{0.2em}dt } _\text{partie négative} \hspace{0.2em} + \hspace{0.2em} \int_{0}^b f(t) \hspace{0.2em}dt $$
Soit deux fonctions \(f,g\) continues sur \(I = [a,b]\), et pour tout \( x \in I, \enspace f(x) \leqslant g(x) \).
Alors,
$$ f(x) \leqslant g(x) \hspace{0.2em} \Longleftrightarrow \hspace{0.2em} f(x) - g(x) \leqslant 0 $$
Avec la propriété de positivité de l'intégrale, on a :
$$ \int_{a}^b f(t) - g(t) \hspace{0.2em}dt \leqslant 0 $$
Ensuite, avec la propriété de linéarité de l'intégrale, on a :
$$ \int_{a}^b f(t) \hspace{0.2em}dt - \int_{a}^b g(t) \hspace{0.2em}dt \leqslant 0 $$
Soit finalement,
$$ \forall (a,x, b) \in D_f^3, \enspace x \in [a, b], $$
$$ \forall x \in I, \enspace f(x) \leqslant g(x) \hspace{0.2em} \Longrightarrow \hspace{0.2em} \int_{a}^b g(t) \hspace{0.2em}dt \leqslant \int_{a}^b f(t) \hspace{0.2em}dt $$
Il s'agit plutôt ici d'une proposition-définition.
La valeur moyenne d'une intégrale sur un intervalle \( [a,b]\) vaut :
$$ \forall (a,b) \in D_f^2, $$
$$ \mu = \frac{1}{(b-a)} \int_{a}^b f(t) $$
Soit une fonction \(f\) continue sur \(I = [a,b]\), un réel \(c \in I\).
Sa primitive \(F\) est elle-même continue, puisque toute fonction dérivable sur un intervalle est continue sur cet intervalle.
Or, avec le théorème des accroissements finis, on sait que :
Pour une fonction \(f\) continue sur \(I = [a,b]\) et dérivable sur \(]a,b[\),
$$ \exists c \in \hspace{0.05em} ]a,b[, \enspace f'(c) = \frac{f(b) - f(a)}{b-a}$$
Dans notre cas,
$$ \exists c \in \hspace{0.05em} ]a,b[, \enspace F'(c) = \frac{F(b) - F(a)}{b-a}$$
Or,
$$ F(b) - F(a) = \int_{a}^b f(t) \hspace{0.2em}dt $$
Soit,
$$ \forall (a,b) \in D_f^2, $$
$$ \exists c \in \hspace{0.05em} ]a,b[, \enspace f(c) = \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt$$
On sait que l'interprétation géométrique de l'intégrale d'une fonction entre deux bornes \(a\) et \(b\) est le fait qu'elle soit égale à l'aire entre la courbe de la fonction et l'axe des abscisses, tel que le montre la figure suivante :

Le résultat précédent nous permet de voir qu'il existera au moins un réel \( c \in \hspace{0.05em} ]a,b[\) tel que :
$$ f(c)(b-a) = \int_{a}^b f(t) \hspace{0.2em}dt$$
C'est-à-dire que l'intégrale de \( a\) vers \( b \) sera égale à un rectangle formé par \( f(c) \) et \( (b-a) \).
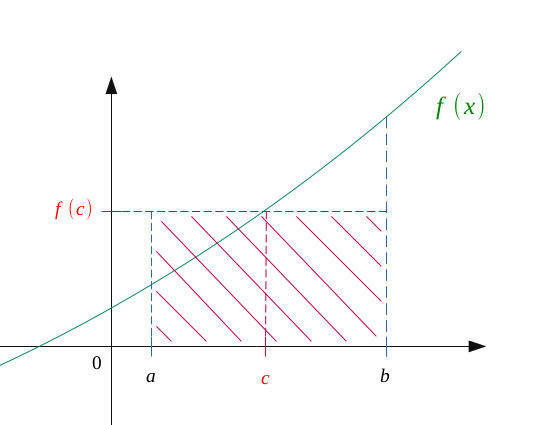
Soit une fonction \(f\) continue sur \(I = [a,b]\).
On introduit les nombres \((m, M) \in \hspace{0.05em} \mathbb{R}^2 \), respectivement les valeurs minimale et maximale de \(f\) sur \(I\), et tels que la figure suivante :
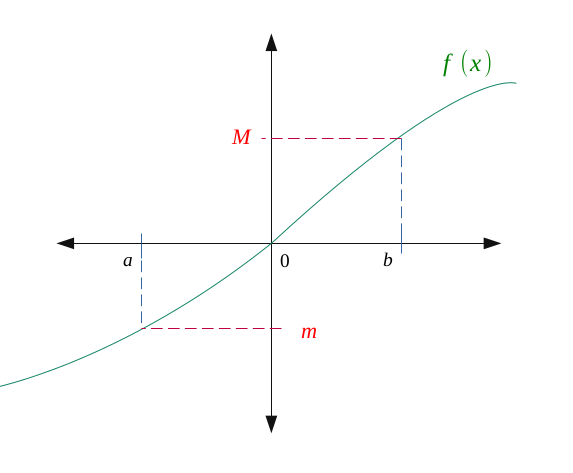
$$ \forall t \in [a,b], \in m \leqslant f(t) \leqslant M $$
Avec la croissance de l'intégrale, on a :
$$ \int_{a}^b m \hspace{0.2em}dt \leqslant \int_{a}^b f(t) \hspace{0.2em}dt \leqslant \int_{a}^b M \hspace{0.2em}dt $$
$$ \Bigl[mt\Bigr]_a^b \leqslant \int_{a}^b f(t) \hspace{0.2em}dt \leqslant \Bigl[Mt \Bigr]_a^b $$
$$ m(b-a) \hspace{0.2em} \leqslant \hspace{0.2em} \int_{a}^b f(t) \hspace{0.2em}dt \hspace{0.2em} \leqslant \hspace{0.2em} M(b-a) $$
$$ m \hspace{0.2em} \leqslant \hspace{0.2em} \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt \hspace{0.2em} \leqslant \hspace{0.2em} M $$
Soit finalement,
$$ \forall (a,b) \in D_f^2, \ \Bigl[ \forall x \in [a, b], \ m = min\{f\}, \ M = max\{f\} \Bigr], $$
$$ m \hspace{0.2em} \leqslant \hspace{0.2em} \frac{1}{(b-a)} \int_{a}^b f(t) \hspace{0.2em}dt \hspace{0.2em} \leqslant \hspace{0.2em} M $$
 Retour en haut de page
Retour en haut de page