








Soit une fonction \(f\) continue sur un intervalle \(I = [a, b]\).
Théorème fondamental du calcul intégral
À partir d'une intégrale définie, il est possible de déterminer une primitive \(S \) de \(f\).
Cette primitive sera la primitive de \(f\) qui s'annule en \(a\) :
$$ S(x)= \int_a^x \ f(t) dt $$
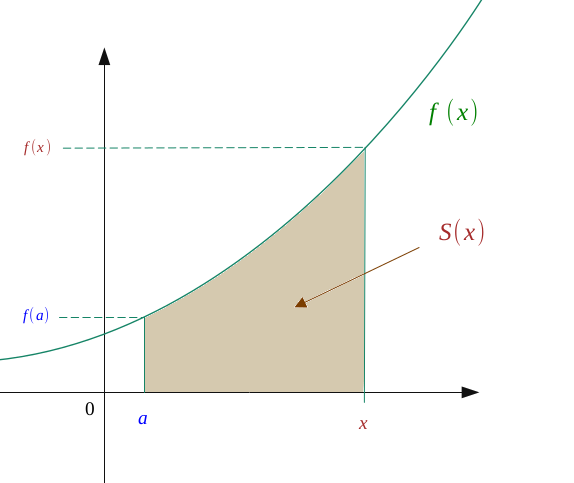
On pourra alors définir une primitive à l'aide de cette intégrale :
$$ F(x) = \int_a^x \ f(t) dt + F(a) $$
Inversement, à partir d'une primitive \(F\) de la fonction \(f\), il est possible de déterminer l'intégrale entre deux bornes \(a\) et \(x\).
$$ \int_a^x \ f(t) dt = F(x) - F(a) $$
Ou plus précisément, pour deux bornes fixes \(a\) et \(b\) :
$$ S_{a,b}= \int_a^b \ f(t) dt = F(b) - f(a) $$
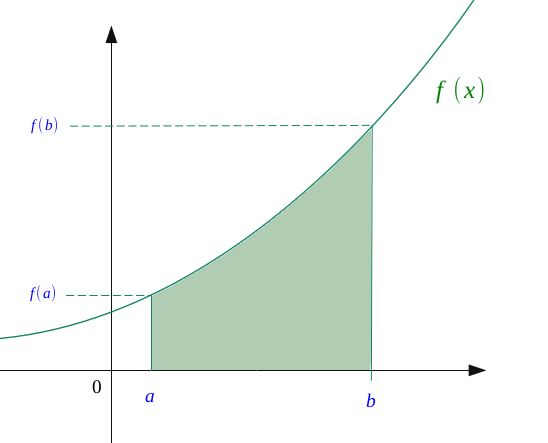
Soit une fonction \(f : x \longmapsto f(x) \) continue, positive et croissante sur un intervalle \(I = [a, b]\).
De même, soit \( n \in \mathbb{N}\) un entier naturel.
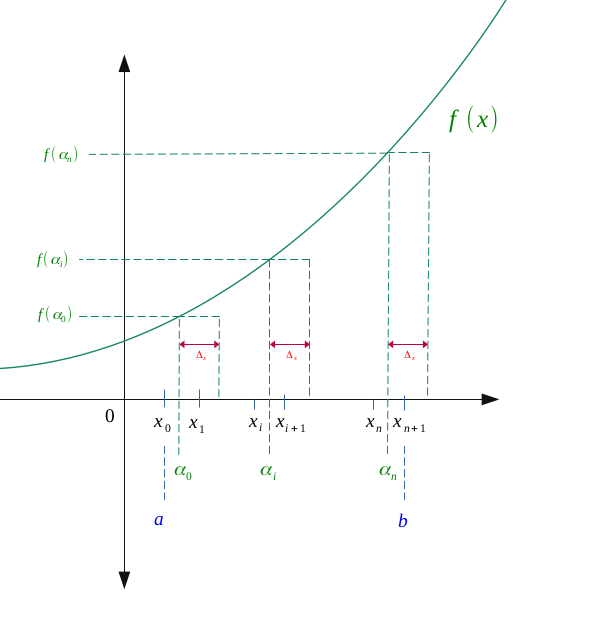
Soit un intervalle \(I = [a,b]\), subdivisons cet intervalle en une série de points \(\bigl \{x_0, \ x_1, \ ...,\ x_i, \ x_{i+1}, \ ..., \ x_{n}, \ x_{n+1} \bigr\} \) théoriquement assez petits, et telle que la figure suivante :
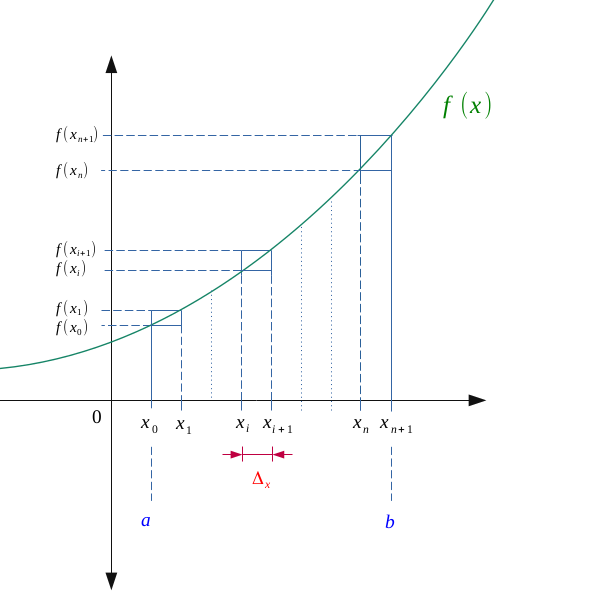
On posera alors \(\Delta_{x} \), la différence formée entre un point et celui d'après :
$$ \forall i \in [\![0, n ]\!], \ \Delta_{x} = x_{i+1}- x_{i} $$
Le théorème des accroissements finis nous dit que :
$$ f \ continue \ sur \ [a,b] \ et \ dérivable \ sur \ ]a,b[ \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a}$$
La fonction \(f\) étant continue sur \([a,b]\) et donc dérivable, on peut lui appliquer ce théorème :
$$\forall i \in [\![0, n ]\!], \ \exists \alpha_i \in \hspace{0.05em} ]x_i, x_{i+1}[, \ f'(\alpha_i) = \frac{ f(x_{i+1}) - f(x_i)}{x_{i+1}-x_{i}}$$
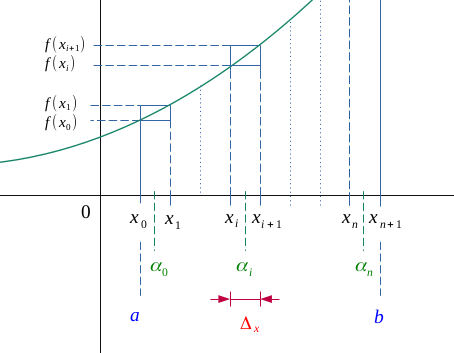
Soit,
$$f'(\alpha_i) \Delta_{x} = f(x_{i+1}) - f(x_i)$$
En faisant la somme de tous ces élément sur l'intervalle \([a,b]\), on a :
$$ \sum_{i=0}^n f'(\alpha_i) \Delta_{x} = \sum_{i=0}^n \Bigl[ f(x_{i+1}) - f(x_i) \Bigr]$$
Or, on sait que lorosqu'on est face à des sommes récurrentes, il va se produire un téléscopage.
$$\sum_{k=0}^n \bigl [ a_{k+1} - a_k \bigr] = \underbrace{a_{n+1}} _\text{premier terme} - \underbrace{a_{0}} _\text{dernier terme} $$
Soit dans notre cas :
$$ \sum_{i=0}^n \Bigl[ f(x_{i+1}) - f(x_i) \Bigr] = f(x_{n+1}) - f(x_0) $$
D'où,
$$ \sum_{i=0}^n f'(\alpha_i) \Delta_{x} = f(x_{n+1}) - f(x_0) $$
Mais par hypothèses de départ, on a :
$$ \Biggl \{ \begin{align*} f(x_0) = f(a) \\ f(x_{n+1}) = f(b) \end{align*} $$
Alors,
$$ \sum_{i=0}^n f'(\alpha_i) \Delta_{x} = f(b) - f(a) $$
Aà présent, on peut remplacer chaque fonction par sa primitive respective et :
$$ \sum_{i=0}^n f(\alpha_i) \Delta_{x} = F(b) - F(a) $$
En passant maintenant à la limite quand \(n \to \infty\), c'est-à-dire un nombre infini de subdivision de l'intervalle \([a,b]\), on a :
$$ lim_{n \to \infty} \ \sum_{i=0}^n f(\alpha_i) \Delta_{x} = lim_{n \to \infty} \ F(b) - F(a) $$
$$ \sum_{i=0}^n f(\alpha_i) dx = F(b) - F(a) \qquad (quand \ n \to \infty, \ \Delta_{x} \to dx) $$
Le terme de gauche correspond à l'intégrale de \(a\) vers \(b\).
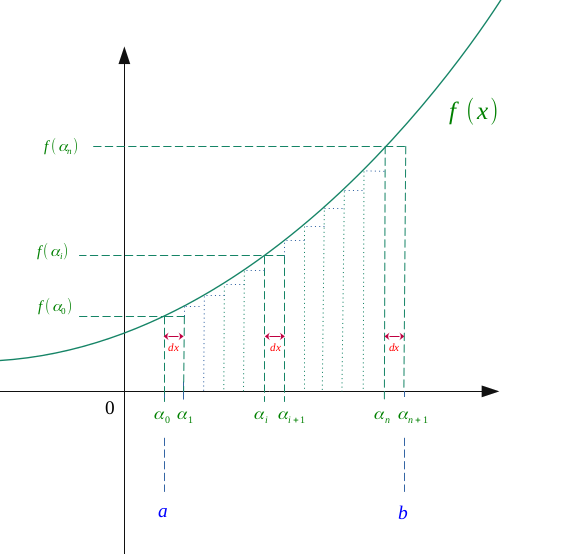
Par ailleurs, on s'aperçoit que :
$$ \forall i \in [\![0, n ]\!], \ n \to \infty \Longrightarrow \Biggl \{ \begin{align*} \alpha_i \to x_i \Longrightarrow (\alpha_0 \to a, \enspace \alpha_{n+1} \to b)\\ f(\alpha_i) \to f(x_i) \Longrightarrow \Bigl(f(\alpha_0) \to f(a), \enspace f(\alpha_{n+1}) \to f(b)\Bigr) \end{align*}$$
On obtient alors l'aire complète entre l'axe des abscisses et la courbe de \(f\) sur l'intervalle \([a,b]\).

On appellera \( S_{a,b} \) l'intégrale définie de la fonction \( f \) dans l'intervalle \([a, b]\), et on la notera :
$$ S_{a,b}= \int_a^b \ f(t) dt = F(b) - f(a) $$
La notation \( \int \) symbolise historiquement la notion de somme, établissant alors un lien entre l'intrégale d'une fonction et sa primitive.
C'est la raison pour laquelle on utilise cette notation pour les primitives, on peut aussi parler d'intégrale non définie, et on notera cette famille de primitives, toutes égales à une constante près :
$$ \int^x \ f(x) dx $$
À présent, considérons une borne supérieure variable \(x\).
Pour éviter toute confusion entre \(x\), la variable de la fonction \(f(x)\), et \(x\) la variable représentant la borne supérieure variable de l'intégrale, il est préférable d'introduire une nouvelle variable \(t\) dans l'intégrande, on aura :
$$ S(x)= \int_a^x \ f(t) dt $$

Cette fonction de \(x\) est alors la primitive de \(f\) qui s'annule en \(a\).
Le paramètre \(t\) étant ici une variable muette, qui disparaîtra après intégration. Par ailleurs, on pourra utiliser \(t\) ou tout autre variable, toutes ces écritures sont équivalentes :
$$ S(x)= \int_a^x \ f(t) \ dt = \int_a^x \ f(u) \ du = \int_a^x \ f(\phi) \ d \phi \ ... etc.$$
Avec ce qui a été vue plus haut, on a alors pour une intégrale définie :
$$ \int_a^x \ f(t) dt = F(x) - F(a) $$
On pourra alors définir une primitive avec cette intégrale qui s'annule en \(a\) :
$$ F(x) = \int_a^x \ f(t) dt + F(a) $$
Si l'on sait calculer l'intégrale définie d'une fonction \(f\) continue sur un intervalle \([a, x]\), on sait trouver une primitive de \(f\).
Inversement, en trouvant une primitive de \(f\), on sait calculer l'intégrale définie sur tout intervalle \([a, x]\).
Même si dans la pratique, il est plus facile de trouver une primitive, puis de calculer son intégrale que le contraire.
Nous allons étudier l'intégrale suivante de la fonction \(f : x \longmapsto x^2\).
$$ S(x)= \int_a^x \ t^2 \ dt $$
La fonction \(f\) est continue et strictement positive sur \([a, x]\).
On a vu que sachant calculer l'intégrale définie d'une fonction \(f\) continue sur un intervalle \([a, x]\), on sait trouver une primitive de \(f\). On va donc pouvoir déterminer une primitive de \(f : x \longmapsto x^2\) sur l'intervalle \([a, x]\).
Et inversement, en trouvant une primitive de \(f\), on sait calculer l'intégrale définie sur tout intervalle \([a, x]\).
Nous allons alors effectuer ces deux procédés.
Nous allons calculer l'intégrale \(S(x)\) par la méthode des sommes de Riemann.
Une des façons de faire est de calculer une somme par la gauche.
La méthode des sommes de Riemann en calculant par la gauche nous dit que :
Pour une fonction \(f\) et \(n \in \mathbb{N}\) un entier naturel représentant le nombre de subdivisions de l'intervalle \((x-a)\). On a :
$$ I_n(x)= \biggl(\frac{x-a}{n} \biggr) \sum_{k=0}^{n-1} \Biggl[ f\biggl(a + k \Bigl(\frac{x-a}{n} \Bigr) \biggr) \Biggr] $$
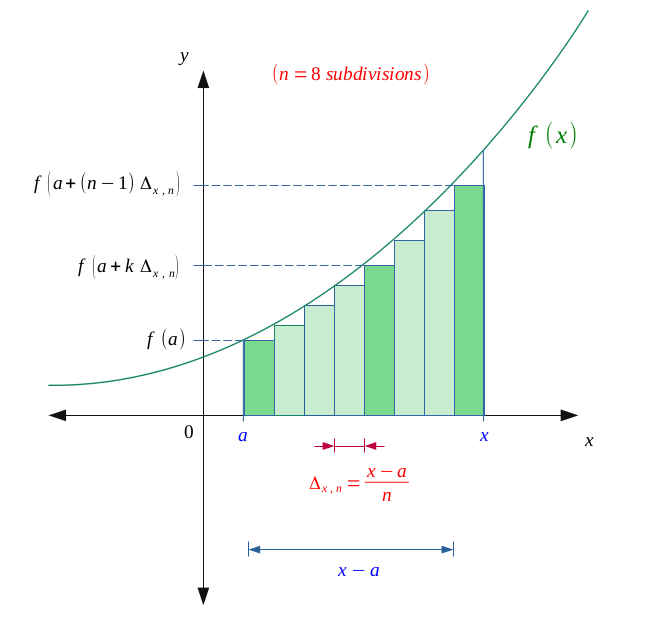
Par simplicité, on peut poser pour le pas la variable \(\Delta_{x, n}\):
$$ \Delta_{x, n} = \frac{x-a}{n} $$
Ce qui donne :
$$ I_n(x)= \Delta_{x, n} \sum_{k=0}^{n-1} \Biggl[ f\bigl(a + k \Delta_{x, n} \bigr) \Biggr] $$
À partir de là, on peut réduire le pas de manière infinitésimal en faisant tendre \(n \to +\infty\).
$$ \int_a^x \ f(t)\ dt = lim_{n \to +\infty} \ \Bigl[ I_n(x) \Bigr] $$
Alors, calculons dans notre cas :
$$ S_n(x)= \Delta_{x, n} \sum_{k=0}^{n-1} \Biggl[ \bigl(a + k \Delta_{x, n} \bigr)^2 \Biggr] $$
$$ S_n(x)= \Delta_{x, n} \Biggl[ a^2 + a^2 + 2a \Delta_{x, n} + \Delta_{x, n}^2 + a^2 + 4a \Delta_{x, n} + 4\Delta_{x, n}^2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} a^2 + 2(n-1)a \Delta_{x, n} + (n-1)^2 \Delta_{x, n}^2 \Biggr] $$
En mettant un peu d'ordre, on a :
$$ S_n(x)= \Delta_{x, n} \Biggl[ (n-1)a^2 + 2a \Delta_{x, n} + 4a \Delta_{x, n} \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} 2(n-1)a \Delta_{x, n} + \Delta_{x, n}^2 + 2^2\Delta_{x, n}^2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} (n-1)^2 \Delta_{x, n}^2 \Biggr] $$
$$ S_n(x)= \Delta_{x, n} \Biggl[ (n-1)a^2 + 2a \Delta_{x, n} \Bigl(1 + 2 + \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} (n-1)\Bigr ) + \Delta_{x, n}^2 \Bigl(1 + 2^2 \hspace{0.2em} + \hspace{0.2em} ... \hspace{0.2em} + \hspace{0.2em} + (n-1)^2 \Bigr) \Biggr] $$
On remarque la présence de la somme des premiers entiers naturels et la somme des premiers carrés d'entiers naturels de \(0\) à \((n-1)\).
$$ S_n(x)= \Delta_{x, n} \Biggl[ (n-1)a^2 + 2a \Delta_{x, n} \Biggl[ \sum_{k=0}^{n-1} k \Biggr] + \Delta_{x, n}^2 \Biggl[ \sum_{k=0}^{n-1} k^2 \Biggr] \Biggr] \qquad (4) $$
Il va falloir adapter ces deux sommes.
La somme des premiers entiers naturels de \(0\) à \(n\) vaut :
$$ \sum_{k = 0}^n k = 1 + 2 \hspace{0.1em} + \hspace{0.1em} ... \hspace{0.1em} + \hspace{0.1em} (n-1) + n \hspace{0.1em} \hspace{0.1em} = \frac{n(n+1)}{2} $$
Alors, de \(0\) à \((n-1)\), cette somme vaut à présent,
$$ \sum_{k = 0}^{n-1} k = \frac{(n-1)n}{2} \qquad (5) $$
De la même manière, on va adapter la somme des premiers carrés d'entiers naturels :
$$ \sum_{k = 0}^n k^2 = \hspace{0.2em} 1 + \hspace{0.2em} 2^2 \hspace{0.1em} + \hspace{0.1em} ... \hspace{0.1em} + \hspace{0.1em} (n-1)^2 + n^2 \hspace{0.1em} \hspace{0.1em} = \frac{n(n+1)(2n+1)}{6} $$
Alors, de \(0\) à \((n-1)\),
$$ \sum_{k = 0}^{n-1} k^2 = \frac{(n-1)n(2n)}{6} \qquad (6) $$
Injectons \( (5) \) et \( (6) \) dans \( (4) \) :
$$ S_n(x)= \Delta_{x, n} \Biggl[ (n-1)a^2 + 2a \Delta_{x, n} \frac{(n-1)n}{2} + \Delta_{x, n}^2 \frac{(n-1)n(2n)}{6} \Biggr] $$
Ce qui équivaut sous une forme développée à :
$$ S_n(x)= \Delta_{x, n}(n-1)a^2 + 2a \Delta_{x, n}^2 \frac{(n-1)n}{2} + \Delta_{x, n}^3 \frac{(n-1)n(2n)}{6} $$
$$ S_n(x)= \Delta_{x, n}(n-1)a^2 + 2a \Delta_{x, n}^2 \frac{(n^2 -n)}{2} + \Delta_{x, n}^3 \frac{(2n^3 - n^2)}{6} $$
À ce stade, remplaçons \( \Delta_{x, n} \) par sa valeur.
$$ S_n(x)= \frac{x-a}{n}(n-1)a^2 + 2a \biggl( \frac{x-a}{n}\biggr)^2 \frac{(n^2 -n)}{2} + \biggl( \frac{x-a}{n} \biggr)^3 \frac{(2n^3 - n^2)}{6} $$
$$ S_n(x)= a^2(x-a) \biggl[ \frac{n-1}{n} \biggr] + a(x-a)^2\biggl[ \frac{n^2 -n}{n^2} \biggr] + \frac{1}{6}(x-a)^3 \biggl[ \frac{2n^3 - n^3}{n^3} \biggr] $$
En passant à la limite quand \(n \to +\infty\) :
$$ S(x)= \int_a^x \ t^2 \ dt = lim_{n \to +\infty} \ S_n(x) $$
$$ S(x)= a^2(x-a) + a(x-a)^2+ \frac{1}{3}(x-a)^3 $$
$$ S(x)= a^2x - a^3 + a(x^2 - 2ax + a^2)+ \frac{1}{3}(x^3 - 3x^2 a + 3 xa^2 -a^3) $$
$$ S(x)= a^2x - a^3 + ax^2 - 2a^2x + a^3+ \frac{x^3}{3} -x^2 a + xa^2 - \frac{a^3}{3} $$
$$ S(x)= \frac{x^3}{3} - \frac{a^3}{3} + \hspace{0.2em} \underbrace { a^2x + xa^2 - 2a^2x } _\text{ \( = 0\)} \hspace{0.2em} + \hspace{0.2em} \underbrace { a^3 - a^3 } _\text{ \( = 0\)} \hspace{0.2em} + \hspace{0.2em} \underbrace { ax^2 + -x^2 a } _\text{ \( = 0\)} $$
$$ S(x)= \int_a^x \ t^2 \ dt = \frac{x^3}{3} - \frac{a^3}{3} \qquad (7) $$
$$ S(x)= \int_a^x \ t^2 \ dt = F(x) - F(a)$$
On a déterminé la primitive générale \(F\) de la fonction \(f\), et celle-ci vaut :
$$ F(x) = \int^x \ t^2 \ dt = \frac{x^3}{3} $$
La primitive générale d'une fonction de type \( x^n \) peut se calculer avec la formule :
$$ \int^x t^n \ dt = \frac{1}{n+1} x^{n+1} $$
Alors, pour notre fonction d'étude \(f : x \longmapsto x^2\), on a comme primitive générale :
$$ \int^x t^2 \ dt = \frac{1}{3} x^{3} $$
À partir de cette expression, on peut calculer l'intégrale définie :
$$ S(x) = \int_a^x t^2 \ dt =\frac{x^3}{3} - \frac{a^3}{3} \qquad (7) $$
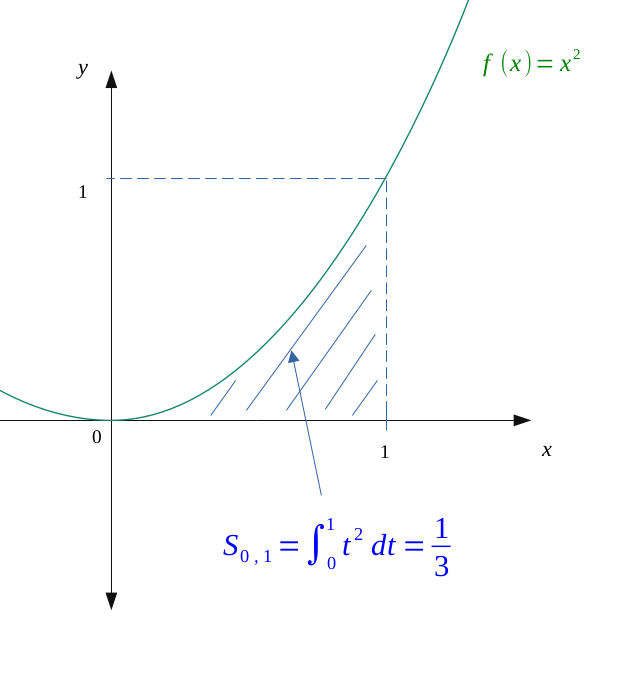
Grâce à l'expression \((7) \) précédemment trouvée, on peut calculer l'aire sous la courbe de la fonction \(f : x \longmapsto x^2\) entre \(0\) et \(1\).
$$ S_{0, 1} = \int_0^1 t^2 \ dt = \Biggl[ \frac{1}{3} x^{3} \Biggr]_0^1 $$
$$ S_{0, 1} = \int_0^1 t^2 \ dt =\frac{1^3}{3} - \frac{0^3}{3} $$
$$ S_{0, 1} =\frac{1}{3} $$
 Retour en haut de page
Retour en haut de page