








Ce théorème est une conséquence directe du théorème de Rolle.
Soit une fonction \(f(x)\) continue sur un intervalle \([a,b]\), et dérivable sur \(]a,b[\).
$$ f \ continue \ sur \ [a,b] \ et \ dérivable \ sur \ ]a,b[ \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a}$$
Soit une fonction \(f(x)\) continue sur un intervalle \([a,b]\), et dérivable sur \(]a,b[\)
Soient de même un réel \( c \in [a,b] \), la tangente \(T_c(x)\) de la courbe de \(f\) au point \(c\), ainsi qu'une fonction affine \(g(x)\) joignant les points \(A\) et \(B\).
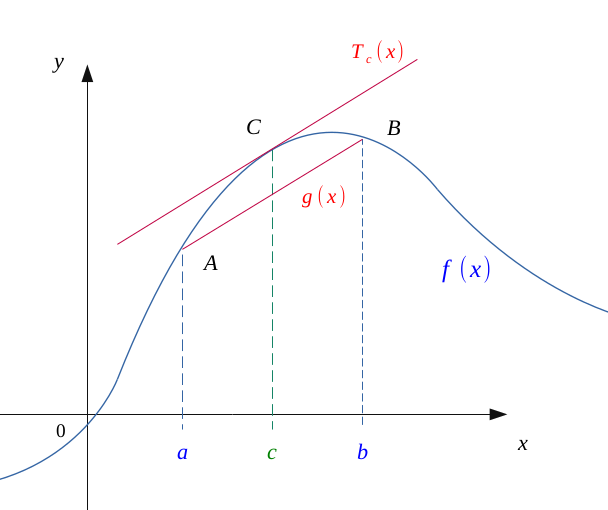
Les points \(A, B, C\) sont les points de la courbe de \(f\) correspondants aux abscisses \(a, b, c\).
Considérons une fonction \(\Phi\) définie de même sur \([a,b]\) telle que :
$$\Phi(x) = f(x) - g(x) \qquad (\Phi) $$
Étant donné que la pente entre \(a\) et un point dans \(x \in [a, b]\) vaut :
$$ \forall x \in [a,b], \ \frac{g(x) - g(a)}{x-a} = \frac{ g(b) - g(a)}{b-a} $$
Or,
$$ \Biggl \{ \begin{align*} f(a) = g(a) \\ f(b) = g(b) \end{align*} $$
Soit,
$$ \frac{g(x) - f(a)}{x-a} = \frac{ f(b) - f(a)}{b-a} $$
$$ g(x) = f(a) + \frac{ f(b) - f(a)}{b-a}(x-a) \qquad (g) $$
Alors, en injectant \((g)\) dans \((\Phi)\),
$$\Phi(x) = f(x) - f(a) - \frac{ f(b) - f(a)}{b-a}(x-a) \qquad (\Phi^*) $$
Les fonctions \( f, g \) étant dérivables sur \( ]a, b[ \), elle sont dérivables sur ce même intervalle, il en sera de même pour \(\Phi\).
Et comme :
$$\Phi(a) = \Phi(b) = 0 $$
Le théorème de Rolle peut alors s'appliquer.
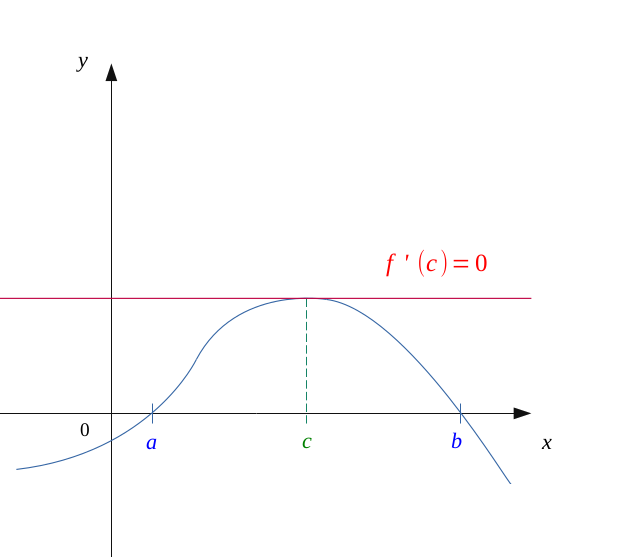
Le théorème de Rolle nous dit que :
Pour une fonction \( f \) continue \( [a, b] \), et dérivable sur \(]a, b[\) :
$$ f(a) = f(b) \Longleftrightarrow, \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = 0 $$
Dans notre cas,
$$ \Phi(a) = \Phi(b) \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ \Phi'(c) = 0 $$
Et, en appliquant la dérivée à l'expression \((\Phi^*)\) :
$$ \Phi'(c) = 0 \Longrightarrow f'(c) - \frac{ f(b) - f(a)}{b-a} = 0 $$
Alors,
$$\exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a} $$
Soit finalement,
$$ f \ continue \ sur \ [a,b] \ et \ dérivable \ sur \ ]a,b[ \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a}$$
 Retour en haut de page
Retour en haut de page