








Derivativity is key notion in analysis, because it underlies all physics and science in general.
Let \( f :x \longmapsto f(x) \) be a continuous function.
We do call \( f'(a) \) the derived number from the function \( f \) at point \( (x=a )\) such as
$$ f'(a) = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$
If (and only if) this number is defined, we then say that \( f \) is derivable at point \( a\).
$$ f \ derivable \ at \ point \ a \Longleftrightarrow lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
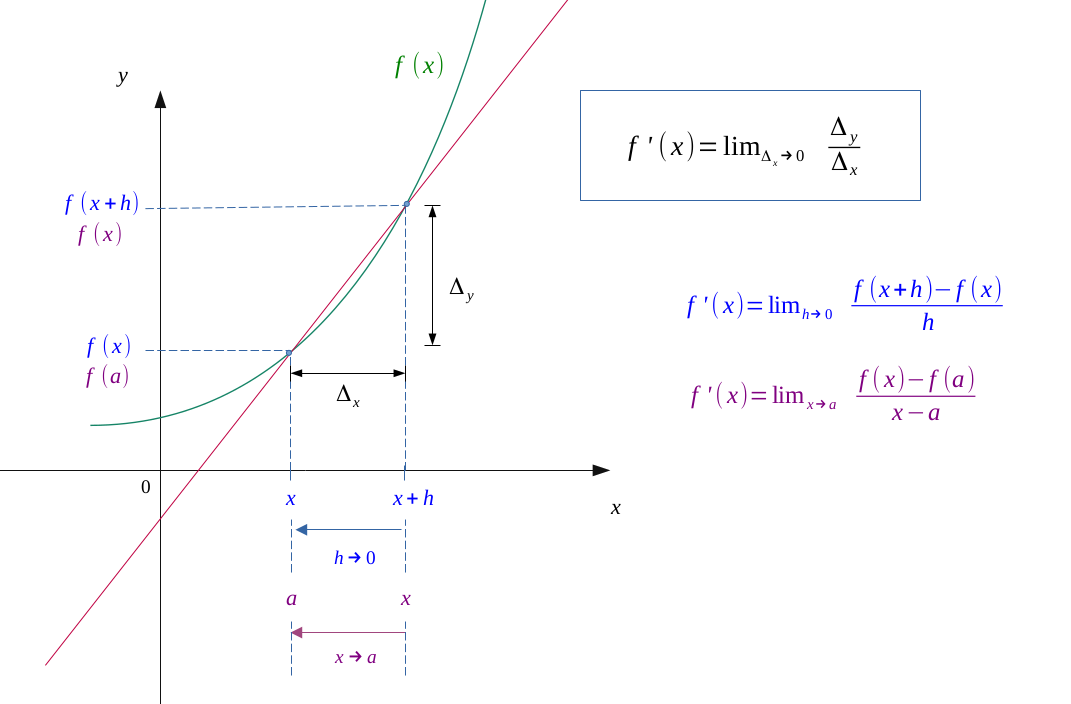
Determining the general expression of the derivative function \(f'\), we will define where the function \(f\) is derivable.
Function \(f'\), derivated from fucntion \( f \) is expressed as follows:
$$ f'(x) = lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$
The is the limit of the rate variation when \( h \to 0 \).
It can also be found in this form:
$$ f'(x) = lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$
At this point, it will be the limit of rate variation when \( x \to a \).
Derivativity implies continuity
$$ f \ derivable \ at \ point \ a \ \Longrightarrow f \ continuous \ at \ point \ a $$
The sign of the derivative indicates the variation
$$ \forall x \in [a,b], \ f'(x) \geqslant 0 \ \Longleftrightarrow f \ increasing \ on \ [a,b] $$
$$ \forall x \in [a,b], \ f'(x) \leqslant 0 \ \Longleftrightarrow f \ decreasing \ on \ [a,b] $$
Equation of the tangent to the curve at point a
We saw in the definition of the derivative that the derived number correspond to the slope of the tangent to the curve of a function.
This line admits for equation at the point of abscissa \(a\):
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
Furthermore, in the case of a convex function (resp. concave), this tangent is always below (resp. above) the curve.
$$f \enspace convex \enspace on \enspace [a,b] \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a)$$
$$f \enspace concave \enspace on \enspace [a,b] \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a) $$
Link between Taylor series of order 1 and derivativity
$$ f \ derivable \ at \ point \ a \ \Longleftrightarrow \ f \ admits \ a \ Taylor \ series \ of \ order \ 1 \ at \ point \ a$$
Let \( f :x \longmapsto f(x) \) be a function, continuous on an interval \( [a, \ a +h] \).
Let us mark two points on the abscissa axis, \( a \) and \( a +h \) (\( h \) being a relatively short distance). Their respective image being \( f(a) \) and \( f(a + h) \), we obtain two points: \( A(a; f(a)) \) and \( B(a + h; f(a + h)) \).
On the following figure, we also drawn the straight line joinin them.
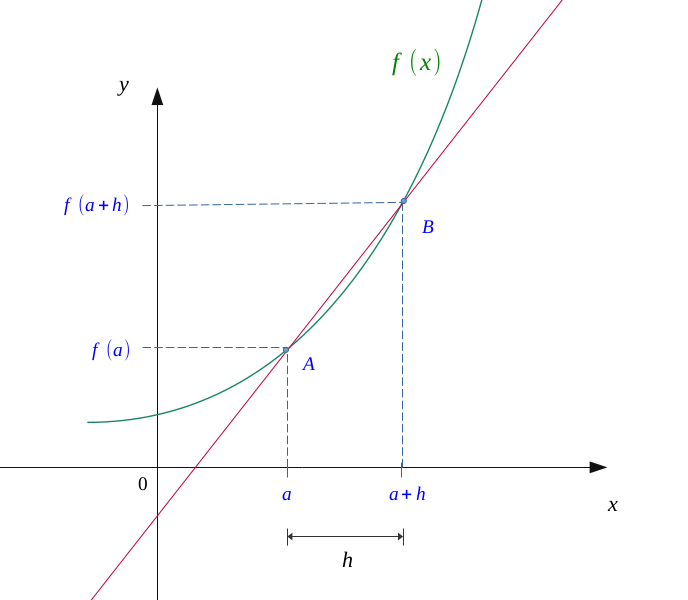
Now we can calculate a mean variation of this function between \( A \) and \( B \).
We can calculate this slope by the following formula:
$$ m = \frac{ \Delta _y}{\Delta _x}$$
$$ m = \frac{ y_B- y_A}{x_B- x_A}$$
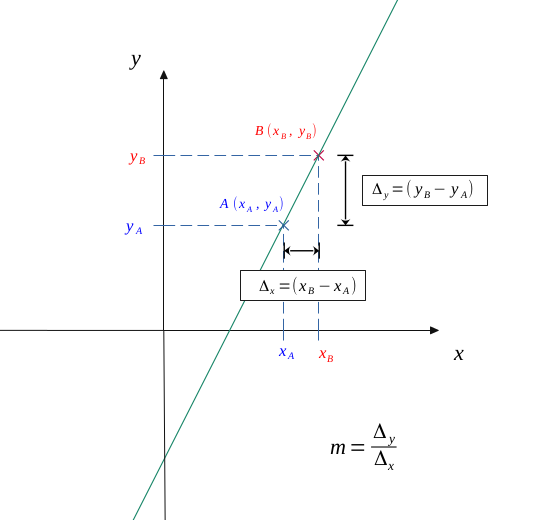
In our case, this gives:
$$ m = \frac{f(a+h) - f(a)}{ a + h -a} $$
So:
$$ m = \frac{f(a+h) - f(a)}{h} \qquad (1) $$
Let us gradually reduce the distance \( h \) which separates our two points on the abscissa axis, making tend \(A\) towards \(B\).
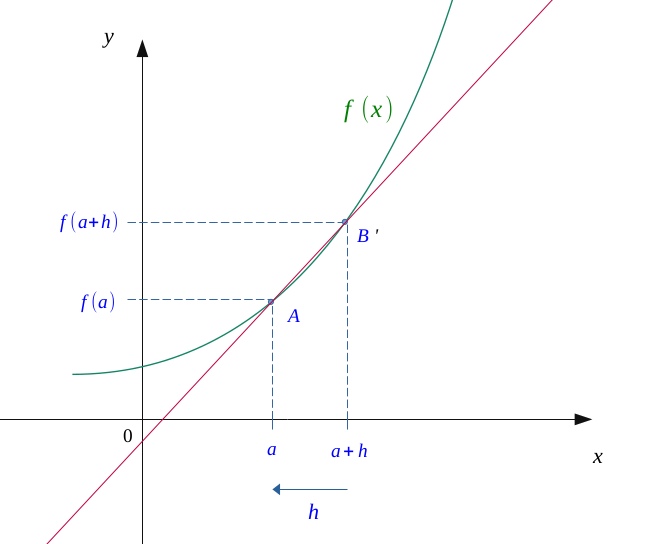
We see that the values of \( a \) and \( a + h \) started to get closer, and the line which connects \( A \) and \( B \) begin to draw a tangent to the curve.
In the same way, we will further reduce the distance \( h \), the latter begins to reduce it to \( 0 \).
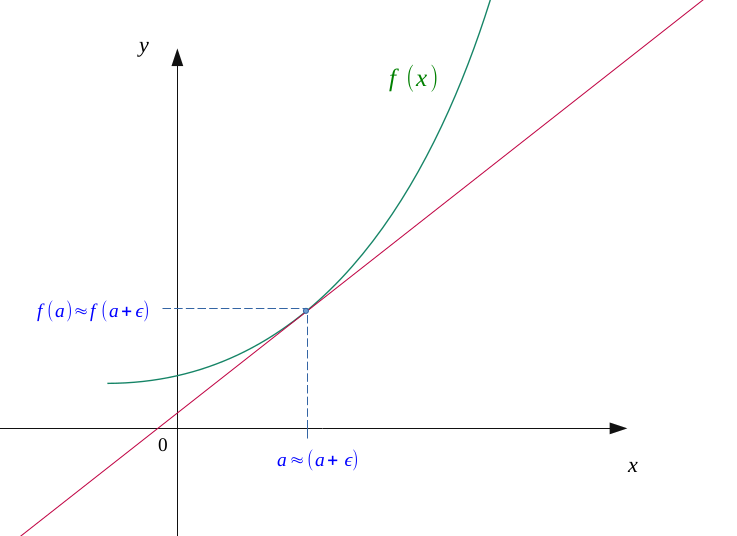
We now see that our two points \( A \) and \( B \) are almost coincident, and that we obtain an almost perfect tangent to the curve at the point of abscissa \( a \).
By imaginating that \( h \) becomes smaller and smaller approching to \( 0 \), our formula \( (1) \) can be expressed as a limit:
$$ m = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h} $$
This number \( m\) obtained, for a \( a \) arbitrarily chosen, will be called the derived number of the function \( f \) at point \( a \). It will be noted \( f'(a) \).
$$ f'(a) = lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}$$
If this number cannot be calculated, the derivative is not defined at this point \( a \).
Now, if (and only if) this number is defined, we will then say that \( f \) is derivable at point \( (x = a) \).
$$ f \ derivable \ at \ point \ a \Longleftrightarrow lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
Determining the general expression of the derivative function \(f'\), we will define where the function \(f\) is derivable.
By generalizing it, that is to say for all \( x \), we call \( f' \) the derivative function of the function \( f \).
$$ f'(x) = lim_{h \to 0} \enspace \frac{f(x+h) - f(x)}{h} $$
The definition set of \( f' \) will then depend of its expression, and will be restricted to the definition set of the function \( f \).
For example, the function \( ln(x) \) is only defined on \(\mathbb{R^*_+}\).
Then, its derivative function:
$$ ln(x)' = \frac{1}{x} $$
is also restricted (a minima) to this interval, whereas the function \( f: x \longmapsto \frac{1}{x} \) is usually defined on \(\mathbb{R^*}\), which is a larger interval.
We say that the derivative is the limit of the variation rate when \( h \) goes to \( 0 \).
We will also find it through this form:
$$ f'(x) = lim_{x \to a} \enspace \frac{f(x) - f(a)}{x - a} $$
At this stage, it will be the limit of the variation rate when \( x \to a \).

In physics, we can also use Leibniz's differential notation \( \frac{df}{dx} \), or that of Newton \( \overset{.}{f} \).
Especially for integral calculus, it is convenient to use Leibniz's.
We saw above that if a function can be derivated at point \( a\), tehen:
$$ lim_{h \to 0} \enspace \frac{f(a+h) - f(a)}{h}= f'(a) \in \mathbb{R} $$
And as a result,
$$ lim_{h \to 0} \ f(a+h) = hf'(a) + f(a) $$
$$ lim_{h \to 0} \ f(a+h) = f(a)$$
Which implies a continuity of the function \( f \) at point \( x = a\).
$$ f \ derivable \ at \ point \ a \ \Longrightarrow f \ continuous \ at \ point \ a $$
Let \(f\) be a positive continuous function on \([a,b]\), and derivable on \( \hspace{0.1em} ]a,b[\).
Now let \( (x_1, x_2) \in \hspace{0.1em} ]a,b[ \), be two inner points of \( \hspace{0.1em} ]a,b[\) in this order.
According to the mean value theorem:
$$ f \ continuous \ on \ [a,b] \ and \ derivable \ on \ ]a,b[ \ \Longrightarrow \ \exists c \in \hspace{0.05em} ]a, b[, \ f'(c) = \frac{ f(b) - f(a)}{b-a}$$
In our case,
$$ \forall (x_1, x_2) \in \hspace{0.1em} ]a,b[ ,$$
$$ \exists x_3 \in \hspace{0.05em} ]x_1, x_2[, \ f'(x_3) = \frac{ f(x_2) - f(x_1)}{x_2-x_1}$$
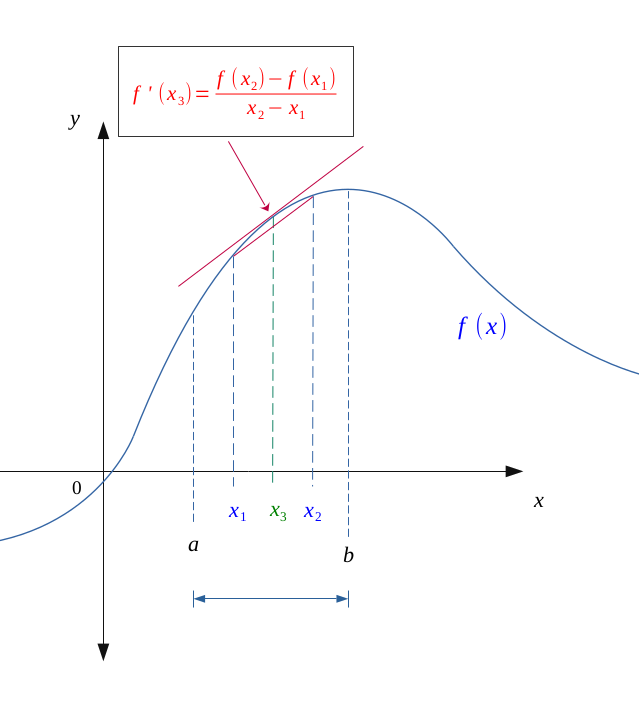
The interval \((x_2-x_1)\) being always positive, if the function \(f\) is increasing on \([a,b]\), it is also the case on \(]x_1, x_2[\), and in this case:
$$ f(x_2) - f(x_1) \geqslant 0 \Longleftrightarrow f'(x_3) \geqslant 0 $$
The derivative function \(f'\) will be therefore positive for all \( x \in [a,b]\).
The same reasoning can be applied for a decreasing function.
$$ \forall x \in [a,b], \ f'(x) \geqslant 0 \ \Longleftrightarrow f \ increasing \ on \ [a,b] $$
$$ \forall x \in [a,b], \ f'(x) \leqslant 0 \ \Longleftrightarrow f \ decreasing \ sur \ [a,b] $$
Let's represent a diagram of a function and its tangent, coming from the derived number at the abscissa point \(a\).
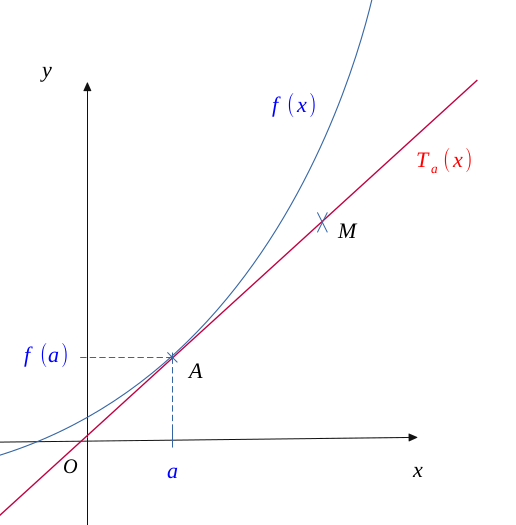
Point \(a\) then has for image \( f(a)\) or \( T_a(a)\)since by definition, a tangent is a point of intersection.
We have also placed a theoretical point \( M(x, T_a(x))\) on the tangent to the curve.
By applying the slope calculation for the points \( A \) and \( B \), we do have:
$$ m = \frac{ \Delta y}{\Delta x}$$
$$ m = \frac{ T_a(x) - T_a(a)}{x - a} \qquad (2) $$
Now, we know that the slope of the tangent to the curve at the abscissa point \( a \) is the same as the derived number in \( a \):
$$ m = f'(a) \qquad (3) $$
So, by injecting \( (3) \) into \( (2) \),
$$ f'(a) = \frac{ T_a(x) - T_a(a)}{x - a}$$
$$ f'(a)(x - a) = T_a(x) - T_a(a) $$
And as \( T_a(a) = f(a) \),
$$ f'(a)(x - a) = T_a(x) - f(a) $$
The tangent to the curve at the abscissa point \(a\) admits for equation:
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
Furthermore, in the case of a convexe function, within any interval \(I = [a, b]\), any rope going on either side of these two points is above the curve.
Its tangent can then only be below:
$$ f(x) \geqslant T_{a}(x) $$
$$f \enspace convex \enspace on \enspace [a,b] \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a)$$
$$f \enspace concave \enspace on \enspace [a,b] \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a)$$
And the inequality will be reversed in the case of a concave function.
We saw above that the equation to the curve at point \(a\) was worth :
$$ T_{a}(x) = f'(a)(x - a) + f(a) $$
Then, we can represent the curve of this tangent \(T_a\), with that of the study function \(f\), and notice that for any point \(M(x, y)\), there is a difference \(\varepsilon_a(x)\) between these two functions.
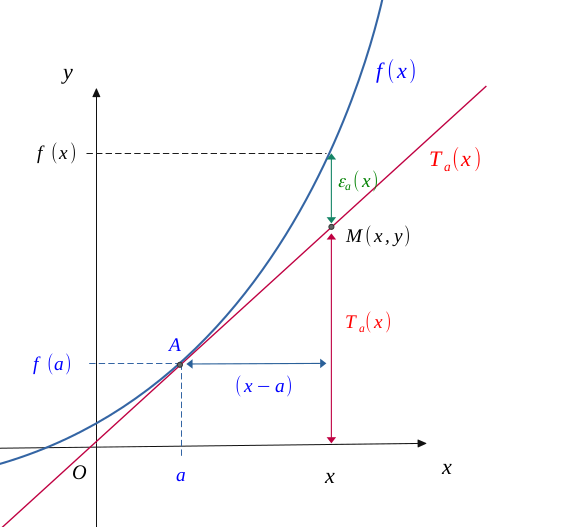
If a function \(f\) admits a Taylor series of order \(1\) at point \(a\) \((TS_n(a))\), then at the neighbourhood of \((x = a)\):
$$ f(x) = f(a) + f'(a)(x-a) + o(x-a) $$
$$ \Bigl( where \enspace o(x-a) = (x-a) \varepsilon(x) \qquad \bigl(with \enspace lim_{x \to a} \ \varepsilon(x) = 0 \bigr) \Bigr) $$
Which implies the existence of \(f'(a)\). So,
$$ f \ admits \ a \ Taylor \ series \ of \ order \ 1 \ at \ point \ a \ \Longrightarrow \ f \ derivable \ at \ point \ a$$
Now, if a function is derivable at point \(a\), as the previous figure clearly illustrates:
$$ \frac{f(x) - f(a)}{x-a} = \frac{T_a(x) + \varepsilon_a(x) - f(a) }{x-a} $$
Replacing \(T_a(x)\) by its value, we do obtain:
$$ \frac{f(x) - f(a)}{x-a} = \frac{f'(a)(x - a) + f(a) + \varepsilon_a(x) - f(a)}{x-a} $$
$$ f(x) - f(a) = f'(a)(x - a) + \varepsilon_a(x)(x-a) $$
And in the end,
$$ f(x) = f(a) + f'(a)(x - a) + \varepsilon_a(x)(x-a) $$
Which is the definition of a Taylor series or order \(1\). Thus,
$$ f \ derivable \ at \ point \ a \ \Longrightarrow \ f \ admits \ a \ Taylor \ series \ of \ order \ 1 \ at \ point \ a$$
The two previous implications give rise to an equivalence, namely:
$$ f \ derivable \ at \ point \ a \ \Longleftrightarrow \ f \ admits \ a \ Taylor \ series \ of \ order \ 1 \ at \ point \ a$$
Let us study the variations of a function \(f\) such as:
$$f(x) = \frac{1}{x} - 2\sqrt{x} $$
This function is only defined on: \( D_f = \ ] 0, +\infty[\).
Calculating its derivative \(f'\), we do have:
$$f(x) = \hspace{0.1em} \underbrace{-\frac{1}{x^2}} _\text{ \( < \hspace{0.2em} 0\)} - \hspace{0.1em} \underbrace{\frac{1}{\sqrt{x}} } _\text{ \( < \hspace{0.2em} 0\)} $$
\(f'(x)\) is always negative on \(D_f\).
Thus, \(f(x)\) will be decreasing on this interval.
|
$$ x $$ |
$$ 0 $$ |
$$ \dots $$ |
$$ +\infty $$ |
|---|---|---|---|
|
$$ sign \ of \ f' $$ |
$$ \bigl ]-\infty \bigr] $$ |
$$- $$ |
$$ \bigl [ 0^- \bigr] $$ |
|
$$ variations \ of \ f $$ |
$$ \bigl [+\infty\bigr] $$ |
$$ \searrow $$ |
$$ \bigl ]-\infty \bigr] $$ |
Furthermore:
$$ \Biggl \{ \begin{align*} lim_{x \to 0} \ f(x) = +\infty \\ lim_{x \to +\infty} \ f(x) = -\infty \end{align*} $$
$$ \Biggl \{ \begin{align*} lim_{x \to 0} \ f'(x) = -\infty \\ lim_{x \to +\infty} \ f'(x) = \hspace{0.1em} 0^- \end{align*} $$
 Go to the top of the page
Go to the top of the page