La convexité d'une fonction

On appelle la convexité d'une fonction $f$ sa forme générale, plutôt en forme de bol (convexe) ou plutôt en forme de cave (concave).

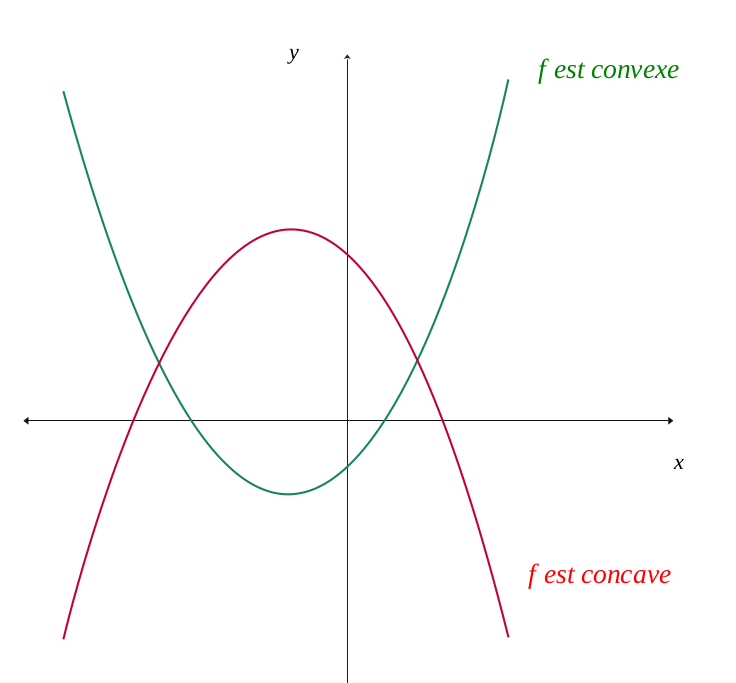
On la définit plus précisément en fonction de la position de ses tangentes et des cordes de la fonction.

Soit une fonction $f$ de classe $ \mathbb{C}^{2}$ sur son ensemble de définition $ D_f $ et un intervalle quelconque $I$.

Le signe de la dérivée seconde indique la convexité

Tout comme la dérivée indique le sens des variations d'une fonction, le signe de la dérivée seconde indique la convexité.

$$ \forall x \in I, $$

$$ f''(x) \geqslant 0 \ \Longleftrightarrow f \ convexe \ sur \ I $$

$$ f''(x) \leqslant 0 \ \Longleftrightarrow f \ concave \ sur \ I $$

Et,

Point d'inflexion : changement de convexité

$$ f''(x) \ change \ de \ signe \ entre \ avant \ et \ apr\textit{è}s \ (x=a) \Longleftrightarrow f \ admet \ un \ point \ d'inflexion \ en \ (x=a) $$

L'inégalité des tangentes

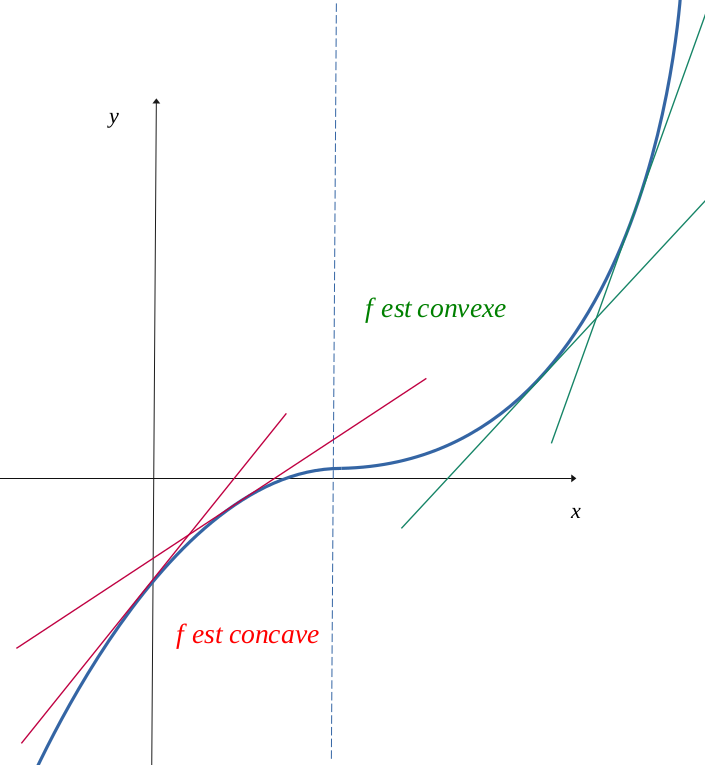
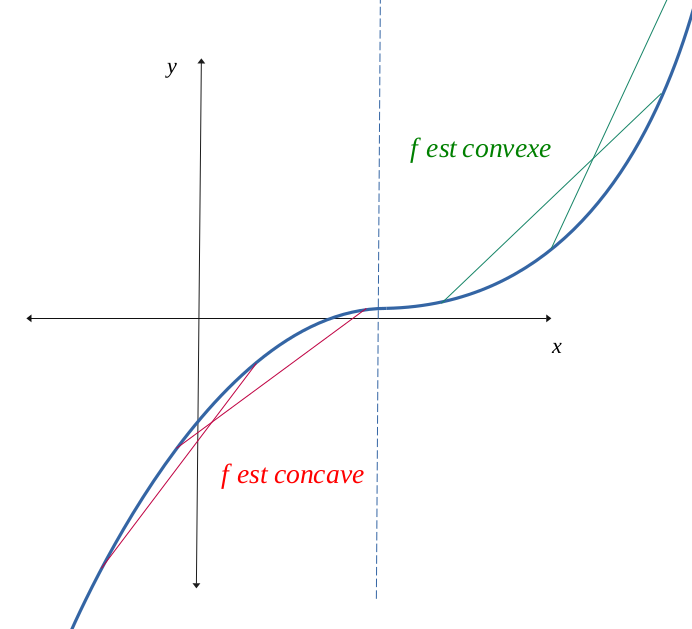
Une fonction $ f $ est dite convexe sur un intervalle $ I $, si toute tangente en un point se situe au-dessous de la courbe. A contrario, elle est concave si toute tangente se situe au-dessus de la courbe.

Illustration de la convexité par la position des tangentes

$$\forall (a, x) \in I^2, $$

$$ f \enspace convexe \enspace sur \enspace I \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a) $$

$$f \enspace concave \enspace sur \enspace I \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a) $$

L'inégalité de convexité

Une fonction $ f $ est dite convexe sur un intervalle $ I $, si toute corde qui relie deux points de cet intervalle se situe au-dessus de la courbe. A contrario, elle est concave si toute corde se situe au-dessous de la courbe.

Illustration de la convexité par la position des cordes

$$ f \enspace convexe \enspace sur \enspace I \Longleftrightarrow \forall (a,b) \in I^2, \enspace \forall \lambda \in [0,1], \enspace f\bigl(\lambda a + (1- \lambda)b \bigr) \hspace{0.2em} \leqslant \hspace{0.2em} \lambda f(a) + (1 - \lambda)f(b) $$

$$f \enspace concave \enspace sur \enspace I \Longleftrightarrow \forall (a,b) \in I^2, \enspace \forall \lambda \in [0,1], \enspace f\bigl(\lambda a + (1- \lambda)b\bigr) \hspace{0.2em} \geqslant \hspace{0.2em} \lambda f(a) + (1 - \lambda)f(b) $$

Démonstrations

Le signe de la dérivée seconde indique la convexité

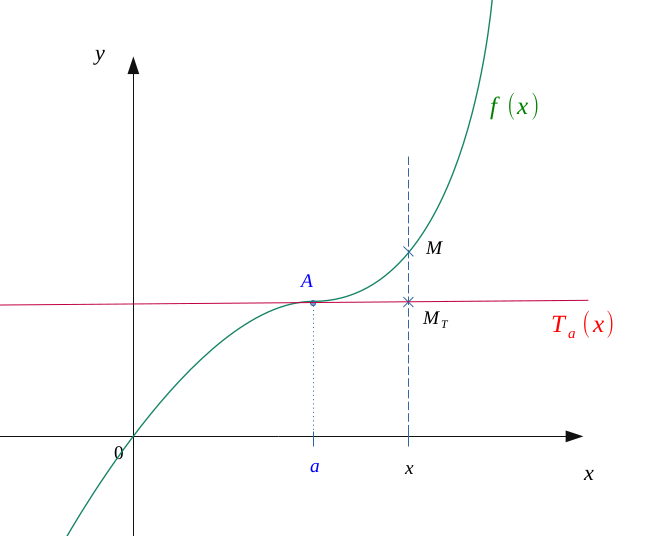
Soit une fonction $f$ de classe $ \mathbb{C}^{2}$ sur son ensemble de définition et sa tangente en point $a$ fixe.

Une fonction et la tangente à sa courbe en un point fixe a

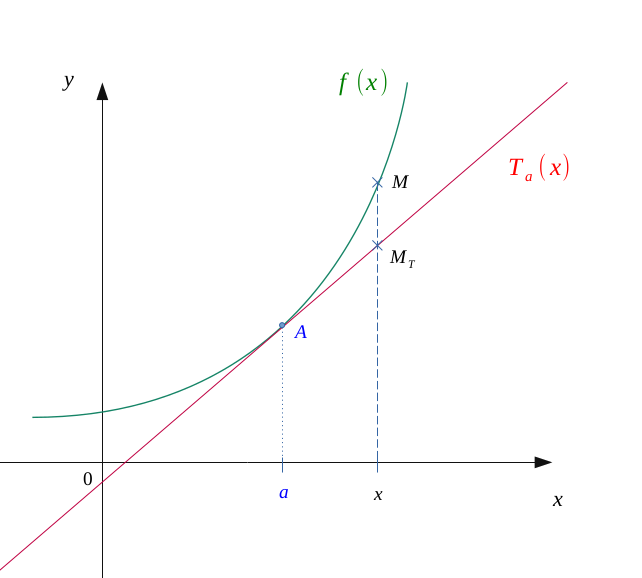
Cherchons à déterminer la position de cette tangente selon la nature de $f$.

Soit deux points $M(x;\ f(x))$ et $M_T(x; \ T_a(x))$ mobiles en fonction de $x$, images respectives de $f$ et celle de $T_a$ au point $x$.

L'équation de la tangente $T_a$ est :

$$ T_{a}(x) = f'(a)(x - a) + f(a) $$

Alors, le point $M_T$ aura pour coordonnées :

$$ M_T(m ; \ f'(a)(m - a) + f(a)) $$

Considérons à présent une nouvelle fonction $g$, différence entre $f$ et $T_a$ :

$$ g(x) = f(x) - T_{a}(x) $$

$$ g(x) = f(x)- f(a) - f'(a)(x - a) \qquad(g) $$

Pour déterminer laquelle des deux se situe au-dessus de l'autre, il faut étudier le signe de $g$ au voisinage de $(x=a)$, valeur pour laquelle la fonction g s'annule.

La fonction $f$ étant dérivable deux fois par hypothèse et $T_a$ étant de classe $ \mathbb{C}^{\infty}$, la fonction $g$ est aussi deux fois dérivable, et :

$$ \Biggl \{ \begin{align*} g'(x) = f'(x) - f'(a) \qquad(g') \\ g''(x) = f''(x) \hspace{5.2em}(g'') \end{align*} $$

Avec $(g)$, $(g')$ et $(g''')$, on aura alors :

$$ (1) \ \Biggl \{ \begin{align*} g(a) = 0 \\ g'(a) = 0 \\ g''(a) = 0 \ \Longleftrightarrow \ f''(a) = 0 \end{align*} $$

Supposition de $ f''(x) > 0$ à gauche et à droite de $a$

Supposons qu'il est possible de trouver un nombre positif $\eta$ tel que :

$$ 0 < |x-a| < \eta \Longrightarrow f''(x) > 0 \qquad(S_+) $$

C'est-à-dire que $f''$ est supposée positive pour les valeurs à gauche et à droite de $a$. À l'exception de $x=a$, comme l'indique bien $(S_+)$ car il peut y avoir des cas où $f''(a)$ sera infinie ou même pas définie du tout.

Cette supposition faite, on voit avec $(g'')$ que, cela entraîne aussi $g'' > 0$ à gauche et à droite de $a$ avec $g''(a) = 0$.

Alors la dérivée $g'$ sera croissante à gauche et à droite de $a$, avec $g'(a) = 0$.

On aura alors à gauche et à droite de $a$ :

$$ \Biggl \{ \begin{align*} \Bigl[ \ x < a \ \Longleftrightarrow \ g'(x) < 0 \ \Bigr] \ \Longleftrightarrow \ g \ d\textit {é}croissante \ pour \ (x < a) \\ \Bigl[ \ x > a \ \Longleftrightarrow \ g'(x) >0 \ \Bigr] \ \Longleftrightarrow \ g \ croissante \ pour \ (x > a) \end{align*} $$

La fonction g avec sa dérivée ainsi que sa dérivée seconde

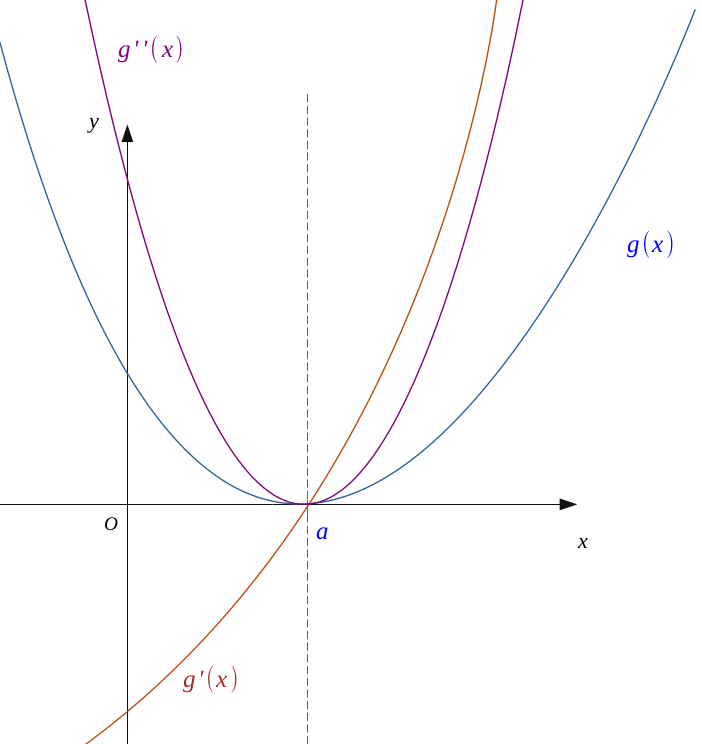
Ce qui entraîne que $g$ est décroissante à gauche et croissante à droite de $a$.

Or $ g(a) = 0$, alors $g > 0$ à gauche et à droite au voisinage de $a$.

On peut en conclure que pour un intervalle $I $ quelconque :

$$ \forall x \in I, \ f''(x) \geqslant 0 \ \Longleftrightarrow f \ convexe \ sur \ I $$

Supposition de $ f''(x) < 0$ à gauche et à droite de $a$

Il est possible de faire la même démonstration en émettant la supposition contraire de $(S_+)$, à savoir :

$$ 0 < |x-a| < \eta \Longrightarrow f''(x) < 0 \qquad (S_-) $$

Alors dans ce cas $g$ sera croissante à gauche et décroissante à droite de $a$, et on aura de la même manière $g < 0$ à gauche et à droite au voisinage de $a$.

$$ \forall x \in I, \ f''(x) \leqslant 0 \ \Longleftrightarrow f \ concave \ sur \ I $$

Supposition d'un signe différent pour $ f''(x)$ à gauche et à droite de $a$

Dans le cas où $ f''(x)$ aurait un signe différent à droite et à gauche de $a$, il existe alors deux cas.

Supposons un premier cas, à savoir que $ f'' < 0$ à gauche et $ f'' > 0$ à droite de $a$. Alors,

$$g''(a) = g'(a) = g(a) = 0 $$

La fonction g avec sa dérivée ainsi que sa dérivée seconde - cas de signes différents

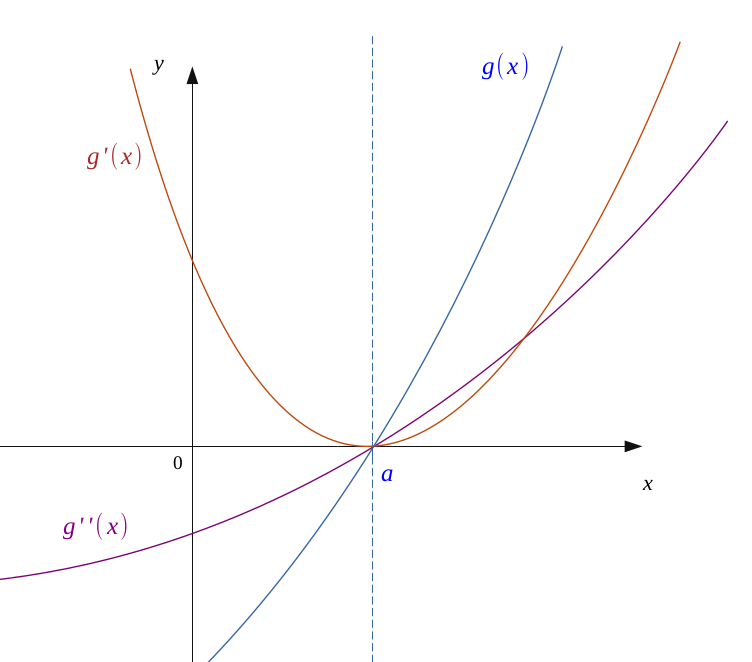
$g'$ sera décroissante à gauche puis croissante à droite, ce qui entraîne $g'(x) > 0$.

Alors $g$ sera toujours croissante et comme $g(a) = 0$, on aura $g(x) < 0$ à gauche et $g(x) > 0$ à droite de $a$.

On aura alors un point d'inflexion au point $a$; c'est-à-dire que $f$ va changer de convexité.

$$ \forall x \in I, \ f''(x) \ change \ de \ signe \ entre \ avant \ et \ apr\textit{è}s \ (x=a) \Longleftrightarrow f \ admet \ un \ point \ d'inflexion \ en \ (x=a) $$

L'inégalité des tangentes

Comme on vient de montrer précédemment que si la fonction $f$ est convexe, alors la courbe de la fonction se situe toujours au dessus de ses tangentes, soit que :

$$ g(x) = f(x)- f(a) - f'(a)(x - a) > 0$$

Alors,

$$\forall (a, x) \in I^2, $$

$$ f \enspace convexe \enspace sur \enspace I \Longleftrightarrow f(x) \geqslant f'(a)(x - a) + f(a) $$

$$f \enspace concave \enspace sur \enspace I \Longleftrightarrow f(x) \leqslant f'(a)(x - a) + f(a) $$

L'inégalité de convexité

Soit $ f $ une fonction continue et convexe sur un intervalle $ I = [a,b] $, et un point $ c \in [a,b] $ de cet intervalle, telle que la figure suivante :

Inégalité de convexité - introduction de lambda

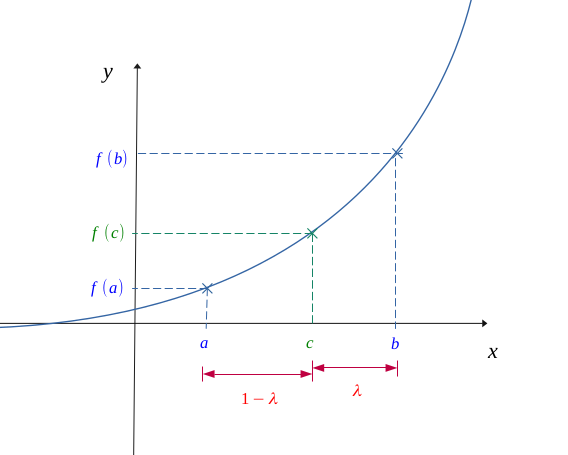
On introduit le réel $\lambda$ proportion entre les points $ c $ et $ b $ par rapport à l'intervalle $ [a,b] $ :

$$ \lambda = \frac{b-c}{b-a} \qquad (\lambda) $$

Par conséquent, on aura l'autre partie qui sera égale à :

$$ 1 - \lambda = \frac{c-a}{b-a} \qquad (1 - \lambda)$$

Sur la figure suivante, on introduit une corde allant de $ a $ vers $ b$ :

Inégalité de convexité - corde de a vers b

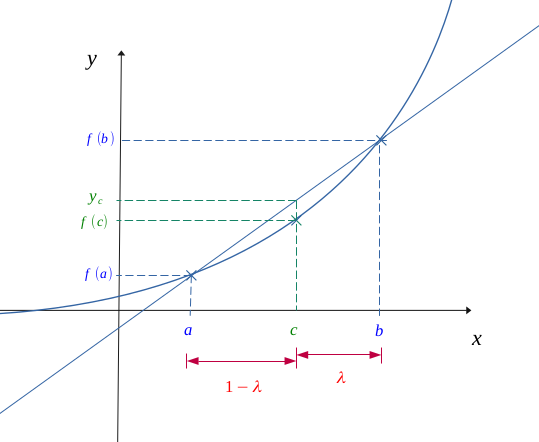
Nous allons pouvoir situer la position de la corde par rapport à la courbe de $ f $ au point $ c $.

On a alors :

Pour la courbe de $ f $

Avec l'équation $ (\lambda)$, on a :

$$ \lambda = \frac{b-c}{b-a} \qquad (\lambda) $$

On effectue un produit en croix :

$$ \lambda (b-a) = b-c $$

$$ c = b - \lambda (b-a) $$

$$ c = b - \lambda b + \lambda a $$

$$ c = \lambda a + (1 - \lambda) b $$

Soit pour $ f(c) $ :

$$ f(c) = f\bigl (\lambda a + (1 - \lambda) b \bigr )$$

Pour la corde allant de $ a $ vers $ b$

En calculant la pente de la corde :

$$ \frac{f(b) - f(a)}{b-a} = \frac{y_c - f(a)}{c-a} $$

$$ (c-a) \frac{f(b) - f(a)}{b-a} = y_c - f(a) $$

Mais :

$$ 1 - \lambda = \frac{c-a}{b-a} \qquad (1 - \lambda)$$

Alors, en le replaçant par sa valeur :

$$ (1 - \lambda) (f(b) - f(a)) = y_c - f(a) $$

$$ f(b) -f(a) - \lambda f(b) + \lambda f(a) = y_c - f(a) $$

$$ y_c = f(b) - \lambda f(b) + \lambda f(a) $$

$$ y_c = \lambda f(a) + (1 - \lambda) f(b) $$

Si la fonction $ f $ est convexe, cela signifie que pour tout point $ c \in [a, b] $, le point de la corde $ y_c $ sera toujours au-dessus de l'image:

$$ f(c) \leqslant y_c $$

Soit finalement,

$$ f \enspace convexe \enspace sur \enspace [a,b] \Longleftrightarrow \forall (a,b), \enspace \forall \lambda \in [0,1], \enspace f\bigl(\lambda a + (1- \lambda)b \bigr) \hspace{0.2em} \leqslant \hspace{0.2em} \lambda f(a) + (1 - \lambda)f(b) $$

On dira que $ f $ est concave si $ (-f) $ est convexe. Soit :

$$\enspace \exists \lambda \in [0,1], \enspace -f\bigl(\lambda a + (1- \lambda)b \bigr) \hspace{0.2em} \leqslant \hspace{0.2em} -\lambda f(a) + ( \lambda - 1)f(b) $$

On multiplie tout par $ -1 $ :

$$f\bigl(\lambda a + (1- \lambda)b \bigr) \hspace{0.2em} \geqslant \hspace{0.2em} \lambda f(a) + ( 1 -\lambda)f(b) $$

$$ f \enspace concave \enspace sur \enspace [a,b] \Longleftrightarrow \forall (a,b), \enspace \forall \lambda \in [0,1], \enspace f\bigl(\lambda a + (1- \lambda)b\bigr) \hspace{0.2em} \geqslant \hspace{0.2em} \lambda f(a) + (1 - \lambda)f(b) $$

Exemples

L'inégalité de convexité

Déterminons la convexité de la fonction $ f : x \longmapsto x^2 $ dans l'intervalle $ [-1,1] $.

Nous allons déterminer s'il existe un intervalle $ \lambda \in [0,1] $ qui vérifie l'une ou l'autre inégalité de convexité.

Membre de la courbe de $ f $

On calcule dans l'intervalle $ [a, b] = [-1,1] $ :

$$ g(\lambda) = f\bigl(\lambda a + (1- \lambda)b\bigr) $$

Soit,

$$ g(\lambda) = (-\lambda + (1- \lambda))^2 = \lambda -2\lambda(1- \lambda) + (1- \lambda)^2 $$

$$g(\lambda) = \lambda -2\lambda + 2\lambda ^2 + 1 -2\lambda + \lambda ^2$$

$$ g(\lambda) =3\lambda^2 - 3\lambda+ 1 $$

Membre de la corde de entre $ -1 $ et $ 1 $

On calcule dans l'intervalle $ [a, b] = [-1,1] $ :

$$ h(\lambda) = \lambda f(a) + (1 - \lambda)f(b) $$

Soit,

$$ h(\lambda) = \lambda (-1)^2 + (1- \lambda) 1^2 = \lambda + 1 -\lambda $$

$$ h(\lambda) = 1 $$

Comparaison de $ g(\lambda) $ et de $ h(\lambda)$

Pour déterminer la position relative de ces deux fonctions, faisons la différence des deux.

Si $ (g-h)(\lambda) > 0$, alors :

$$ (g-h)(\lambda) = 3\lambda^2 - 3\lambda+ 1 - 1 $$

$$ (g-h)(\lambda) = 3\lambda^2 - 3\lambda $$

$$ (g-h)(\lambda) = 3\lambda (\lambda -1) $$

On peut directement faire un tableau de signes.

$$ \lambda $$	$$ -\infty $$	$$ \hspace{3em}$$	$$ 0 $$	$$ \hspace{3em}$$	$$1$$	$$ \hspace{3em}$$	$$ +\infty $$
$$ 3 \lambda $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$	$$ + $$	$$ + $$	$$ + $$
$$ \lambda - 1$$	$$ - $$	$$ - $$	$$ - $$	$$ - $$	$$ 0 $$	$$ + $$	$$ + $$
$$ (g-h)(\lambda) $$	$$ + $$	$$ + $$	$$0 $$	$$ - $$	$$ 0 $$	$$ + $$	$$ + $$

On a bien pour tout $ \lambda \in [0, 1], \enspace (g-h)(\lambda) \leqslant 0$.

Cela signifie que :

$$ g(\lambda) \leqslant f(\lambda) \Longleftrightarrow \bigl[point \enspace de \enspace la \enspace courbe\bigr] \leqslant \bigl[point \enspace de \enspace la \enspace corde \bigr] $$

Les cordes sont au-dessus de la courbe, la fonction est convexe.