







Cette méthode consiste à calculer une certaine valeur plus ou moins connue, mais que l'on souhaiterait approximer plus précisément. La méthode se fait par itération successive.
Soit \( f \) une fonction convexe (resp. concave) et strictement croissante (resp. décroissante) et positive sur un intervalle \( I \) et \( a_0 \) un réel appartenant à \( I \) tel que \( f(a_0) > 0 \) (resp. \( f(a_0) < 0 \)).
La méthode consisite à déterminer le réel \( x_0 \in I \), tel que : \( f(x_0) = 0 \)
Généralement, on va déterminer la valeur de \( x_0 \) pour laquelle \( f \) s'annule sur \( I \).
Et cette valeur équivaut à :
$$ x_0 = lim_{n \to +\infty} \enspace (a_n) $$
Avec \( (a_n)_{n \in \mathbb{N}} \) une suite récurrente telle que :
$$ a_{n + 1} = a_n - \frac{f(a_n)}{f'(a_n)} $$
Soit \( f \) une fonction convexe (resp. concave) et strictement croissante (resp. décroissante) et positive sur un intervalle \( I \) et \( a_0 \) un réel appartenant à \( I \) tel que \( f(a_0) > 0 \) (resp. \( f(a_0) < 0 \)).
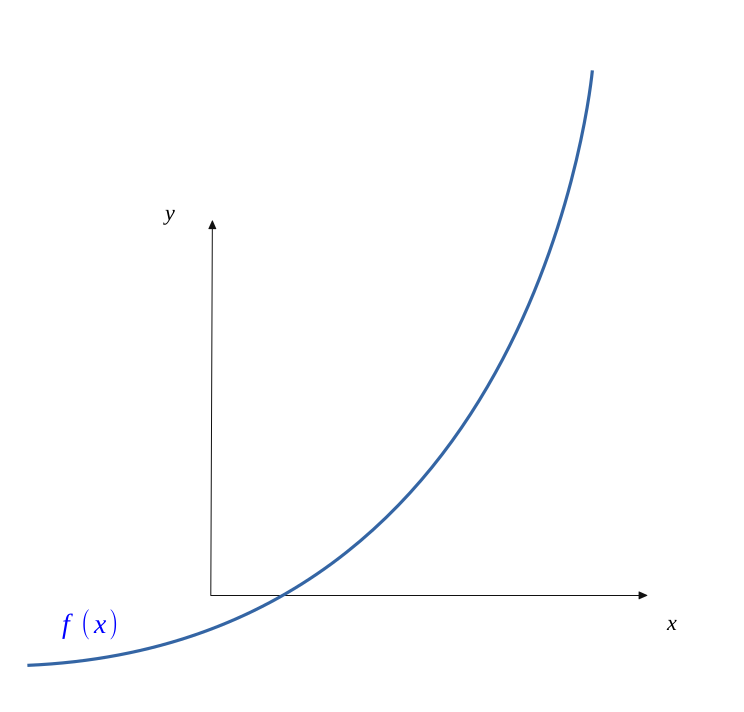
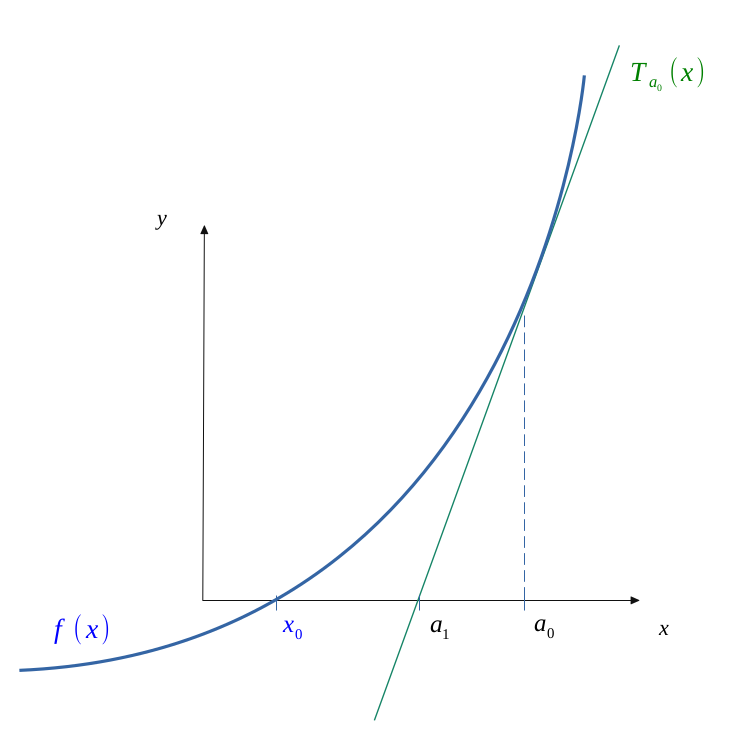
Nous savons que cette fonction va s'annuler à un moment donné, mais nous ne savons pas exactement pour quelle valeur \( x_0 \).
Nous avons représenté la tangente à cette courbe au point \( x = a_0 \), et répondant à l'équation :
$$ T_{a_0}(x) = f'(a_0)(x - a_0) + f(a_0)$$

Nous allons alors chercher à évaluer lorsque cette fonction va s'annuler. On a :
$$ T_{a_0}(x) = 0 $$
$$ f'(a_0)(x - a_0) + f(a_0) = 0 $$
$$ f'(a_0).x - f'(a_0).a_0 + f(a_0) = 0 $$
$$ f'(a_0).x = f'(a_0).a_0 - f(a_0) $$
On sait ici que \( f'(a_0) > 0 \), donc on peut diviser par \( f'(a_0) \).
$$ x = \frac{f'(a_0).a_0 - f(a_0)}{f'(a_0)} $$
$$ x = a_1 = a_0 - \frac{ f(a_0)}{f'(a_0)} $$
Si l'on continue et que l'on fait la même chose ne partant cette fois-ci de \( a_1 \), nous obtiendrons :
$$ a_2 = a_1 - \frac{ f(a_1)}{f'(a_1)} $$
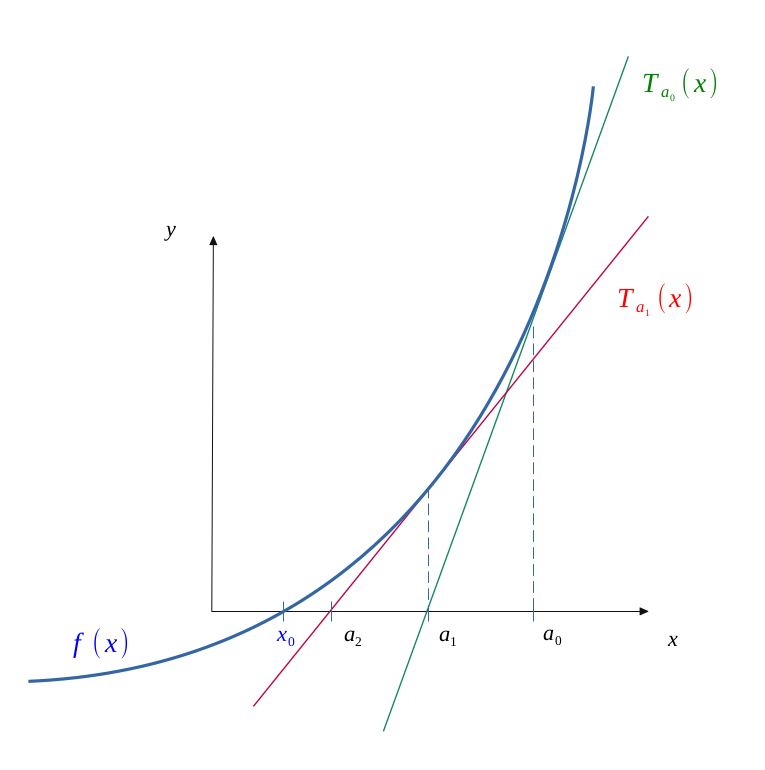
Nous obtenons alors une suite récurrente \( (a_n)_{n \in \mathbb{N}} \) telle que :
$$ \enspace a_{n + 1} = a_n - \frac{f(a_n)}{f'(a_n)} $$
Plus on établira d'itérations successives et plus l'on va tendre vers la valeur souhaitée, soit :
$$ x_0 = lim_{n \to +\infty} \enspace (a_n) $$
Avec \( (a_n)_{n \in \mathbb{N}} \) une suite récurrente telle que :
$$ a_{n + 1} = a_n - \frac{f(a_n)}{f'(a_n)} $$
On pourra réitérer le même raisonnement pour une fonction concave et/ou décroissante et/ou négative, à adpater selon le cas.
Nous allons tenter de chercher une valeur approchée de \( \sqrt{2} \) par cette méthode.
Soit \( f \) une fonction telle que \( x_0 = \sqrt{2}\) soit solution de \( f(x_0) = 0 \). Partons de cette hypothèse et cherchons à déterminer cette fonction.
$$ x_0 = \sqrt{2} $$
$$ x_0^2 = 2 $$
$$ x_0^2 - 2 = 0 $$
Nous allons alors étudier la fonction \( f \) définie par :
$$ f(x) = x^2 - 2 $$
Et ainsi trouver une valeur approchée de \( x_0 \) pour laquelle \( f(x_0) = 0 \).
Nous sommes bien dans le cas d'une fonction convexe et strictement croissante, nous pouvons alors appliquer la méthode.
Il va s'agir de computer les différentes valeurs de la suite :
$$ a_{n + 1} = a_n - \frac{f(a_n)}{f'(a_n)} $$
Avec \( f(x) = x^2 - 2 \) et sa fonction dérivée \( f'(x) = 2x \).
Soit,
$$ a_{n + 1} = a_n - \frac{a_n^2 - 2}{2a_n} $$
Voici le résultat de la computation avec différentes valeur pour \( a_0 \) :
 Retour en haut de page
Retour en haut de page