








Aussi appplé loi des cosinus, le théorème d'Al-Kashi est la généralisation du théorème de Pythagore pour tout triangle. Il s'exprime ainsi :
Dans le contexte d'un triangle quelconque \(\{a, b, c\}\), avec chaque angle \(\alpha, \beta, \gamma \) opposé à sa longueur correspondante, tel que :
$$ \left \{ \begin{gather*} \alpha \enspace oppos \textit{é} \enspace \textit{à} \enspace a \\ \beta \enspace oppos\textit{é} \enspace \textit{à} \enspace b \\ \gamma \enspace oppos\textit{é} \enspace \textit{à} \enspace c \end{gather*} \right \} $$
et tel que la figure suivante :
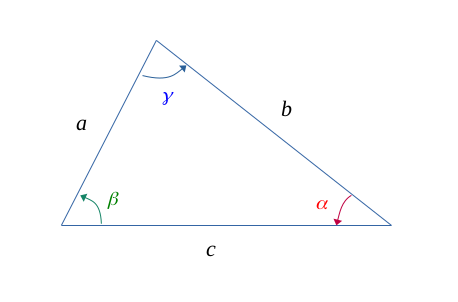
On a les relations suivantes :
$$ a^2 = b^2 + c^2 - 2bc.cos(\alpha) \qquad (Al-Kashi) $$
$$ b^2 = a^2 + c^2 - 2ac.cos(\beta) \qquad (Al-Kashi^*) $$
$$ c^2 = a^2 + b^2 - 2ab.cos(\gamma) \qquad (Al-Kashi^{**}) $$
Dans les démonstrations qui suivent, nous allons démontrer le théorème uniquement sur le premier des trois côtés du triangle. Après cela, les deux autres démonstrations sont triviales.
Pour le démontrer, nous avons projeté sur \( c \) la hauteur \( h_c \) pour obtenir la figure suivante :
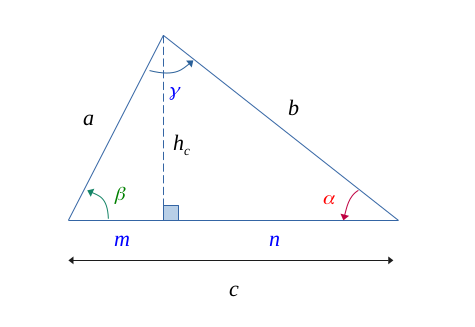
Dans le petit triangle \(\{a, h_c, m\}\), le théorème de Pythagore nous donne :
$$ a^2 = m^2 + h_c^2 $$
$$ a^2 = (c-n)^2 + h_c^2 $$
$$ a^2 = c^2 - 2cn + n^2 + h_c^2 \qquad (1) $$
Or, dans l'autre petit triangle \(\{b, h_c, n\}\),
$$ n^2 + h_c^2 = b^2 \qquad (2) $$
Et aussi,
$$ cos(\alpha) = \frac{n}{b} \Longleftrightarrow n = b.cos(\alpha) \qquad (3) $$
En injectant \((2)\) et \((3)\) dans \((1)\), on a :
$$ a^2 = c^2 - 2cb.cos(\alpha) + b^2 $$
Soit finalement,
$$ a^2 = b^2 + c^2 - 2bc.cos(\alpha) \qquad (Al-Kashi) $$
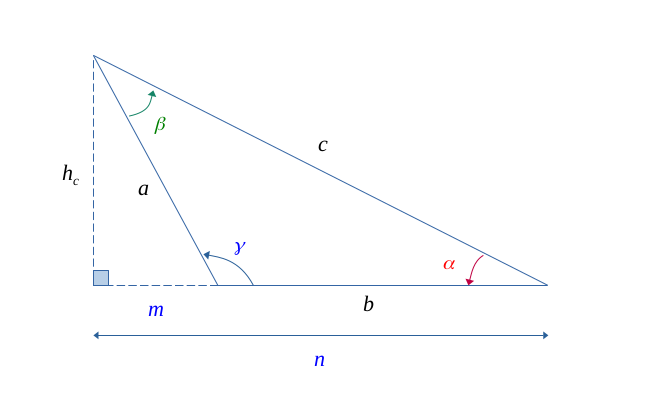
De la même manière, dans le petit triangle \(\{a, h_c, m\}\), le théorème de Pythagore nous donne :
$$ a^2 = m^2 + h_c^2 $$
$$ a^2 = (n-b)^2 + h_c^2 $$
$$ a^2 = n^2 - 2nb + b^2 + h_c^2 \qquad (4) $$
Or, dans le grand triangle \(\{h_c, n, c\}\),
$$ h_c^2 + n^2 = c^2 \qquad (5) $$
Et aussi,
$$ cos(\alpha) = \frac{n}{c} \Longleftrightarrow n = c.cos(\alpha) \qquad (6) $$
En injectant \((5)\) et \((6)\) dans \((4)\), on a :
$$ a^2 = b^2 + c^2 - 2bc.cos(\alpha) \qquad (Al-Kashi) $$
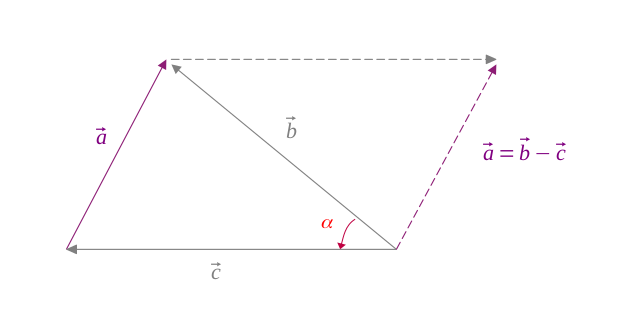
Si l'on considère les longueurs \(a, b, c\) comme trois vecteurs, et telle que la figure suivante :
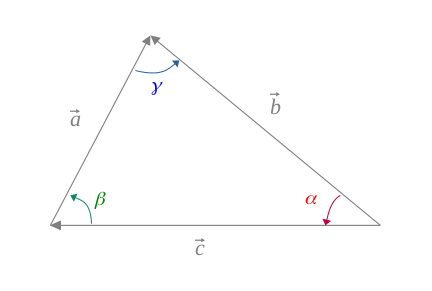
Alors, on a par la relation de Chasles :
$$ \vec{a} = \vec{b} - \vec{c} \qquad (7) $$
Grâce à la propriété de carré scalaire, on sait que :
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = || \vec{u} ||^2$$
Alors, on a :
$$ \vec{a}.\vec{a} = || \vec{a} ||^2$$
En injectant la proposition \((7)\), on obtient alors :
$$ (\vec{b} - \vec{c})^2 = || \vec{a} ||^2$$
De même, avec les identités remarquables du produit scalaire, on a la propriété suivante :
$$ \forall (\vec{u}, \vec{v}), $$
$$ (\vec{u} - \vec{v})^2 = || \vec{u} ||^2 - 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
Soit dans notre cas de figure,
$$ || \vec{b} ||^2 - 2 \vec{b}.\vec{c} + || \vec{c} ||^2 = || \vec{a} ||^2$$
$$ b^2 - 2 bc \ cos(\vec{b}, \vec{c}) + c^2 = a^2 $$
$$ a^2 = b^2 + c^2 - 2bc.cos(\alpha) \qquad (Al-Kashi) $$
Nous avons démontré la première formule du théorème :
$$ a^2 = b^2 + c^2 -2bc.cos(\alpha) \qquad (Al-Kashi)$$
On retrouve alors les deux autres relations en répétant cette démonstration sur les deux longueurs restantes.
$$ b^2 = a^2 + c^2 - 2ac.cos(\beta) \qquad (Al-Kashi^*) $$
$$ c^2 = a^2 + c^2 - 2ab.cos(\gamma) \qquad (Al-Kashi^{**}) $$
 Retour en haut de page
Retour en haut de page