








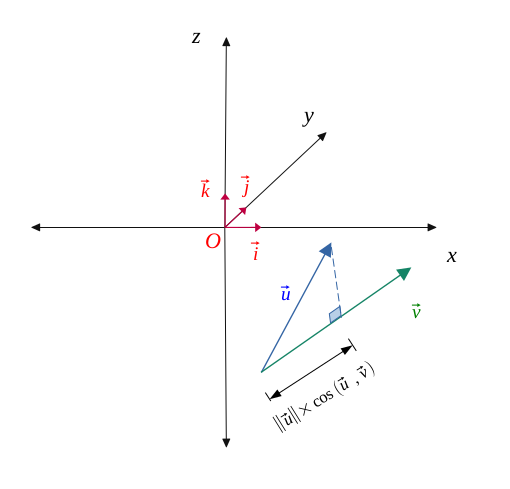
Soient \( \vec{u}\) et \( \vec{v}\) deux vecteurs.
On note \(||\vec{u}|| \) et \(||\vec{v}|| \) les normes respectives des vecteurs \( \vec{u}\) et \( \vec{v}\), et \( (\vec{u} , \vec{v})\) l'angle formé par les deux vecteurs.
On appelle le produit scalaire \( \vec{u}.\vec{v} \), le nombre réel résultant de :
$$ \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) $$
C'est la norme du projeté orthogonal du vecteur \( \vec{u}\) sur le vecteur \( \vec{v}\), multiplié par la norme du vecteur \( \vec{v}\).
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u} . \vec{v} = \vec{v}. \vec{u} $$
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \ et \ \vec{v} \ orthogonaux \Longleftrightarrow \vec{u}. \vec{v} = 0 $$
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = || \vec{u} ||^2 $$
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
$$ \forall \lambda \in \hspace{0.05em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
Par ailleurs, en effectuant le produit scalaire \( (\lambda\vec{u}).(\mu\vec{v})\), on obtient :
$$ \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).(\mu\vec{v}) = |\lambda| \times |\mu| \times \vec{u}. \vec{v} $$
Distributivité par rapport à l'addition
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ \vec{u}.( \vec{v} + \vec{w}) = \vec{u}.\vec{v} + \vec{u}.\vec{w} $$
Et aussi la distributivé à gauche :
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
On a les mêmes formules que les identités remarquables.
$$ \forall (\vec{u}, \vec{v}), $$
$$ (\vec{u} + \vec{v})^2 = || \vec{u} ||^2 + 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
$$ (\vec{u} - \vec{v})^2 = || \vec{u} ||^2 - 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
$$ || \vec{u} ||^2 - || \vec{v} ||^2= (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) $$
Expression en fonction des normes
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( || \vec{u} + \vec{v} ||^2 - || \vec{u} ||^2 - || \vec{v} ||^2 \right ) $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( || \vec{u} ||^2 + || \vec{v} ||^2 - || \vec{u} -\vec{v} ||^2 \right ) $$
Récapitulatif des formules des propriétés du produit scalaire
Soient \(\vec{u} \) et \(\vec{v} \) deux vecteurs.
Pour les deux produits scalaires \( \vec{u}.\vec{v} \) et \( \vec{v}.\vec{u} \), on a :
$$ \Biggl \{ \begin{align*} \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) \\ \vec{v}.\vec{u} = ||\vec{v}|| \times ||\vec{u}|| \times cos(\vec{v}, \vec{u}) \end{align*} $$
Si on appelle \(\alpha \) = \( (\vec{u}, \vec{v}) \), l'angle entre \( \vec{u} \) et \(\vec{v} \), alors :
$$ \Biggl \{ \begin{align*} cos(\alpha ) = cos(\vec{u}, \vec{v}) \\ cos( - \alpha ) = cos(\vec{v}, \vec{u}) \end{align*} $$
Or, la fonction cosinus est paire et : \( \forall \alpha \in \mathbb{R}, \ cos(\alpha ) = cos(-\alpha ) \).
Alors on en déduit que : \( cos(\vec{u}, \vec{v}) = cos(\vec{v}, \vec{u}) \).
Soit finalement,
$$ \forall (\vec{u}, \vec{v}), $$
$$ \vec{u}.\vec{v} =\vec{v}.\vec{u} $$
Soient \(\vec{u} \) et \(\vec{v} \) deux vecteurs différents du vecteur nul.
Partons de l'hypothèse que \(\vec{u} \) et \(\vec{v} \) sont orthogonaux.
Alors, par la définition du produit scalaire,
$$ \vec{u}.\vec{v} = ||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u}, \vec{v}) $$
Mais si \(\vec{u} \) et \(\vec{v} \) sont orthogonaux, alors \(cos(\vec{u}, \vec{v}) = cos \left(\frac{\pi}{2}\right) = 0 \).
Alors leur produit scalaire sera nul, et :
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \ et \ \vec{v} \ orthogonaux \Longrightarrow \vec{u}. \vec{v} = 0 $$
Réciroquement, étant donné que par hypothèse nos deux vecteurs \(\vec{u} \) et \(\vec{v} \) sont différents du vecteur nul, alors :
$$ \vec{u}. \vec{v} = 0 \Longrightarrow cos(\vec{u}, \vec{v}) = 0 $$
Et,
$$ \forall k \in \mathbb{N}, \ cos(\vec{u}, \vec{v}) = 0 \Longrightarrow \Biggl\{ (\vec{u}, \vec{v}) = \frac{k\pi}{2} \Biggr \} $$
Alors, les deux vecteurs \(\vec{u} \) et \(\vec{v} \) sont orthogonaux.
$$\vec{u}. \vec{v} = 0 \Longrightarrow \vec{u} \ et \ \vec{v} \ orthogonaux $$
$$ \forall (\vec{u}, \vec{v}) \neq \vec{0},$$
$$ \vec{u} \ et \ \vec{v} \ orthogonaux \Longleftrightarrow \vec{u}. \vec{v} = 0 $$
Soit un vecteur \(\vec{u} \).
Alors, par la définition du produit scalaire,
$$ \vec{u}.\vec{u} = ||\vec{u}|| \times ||\vec{u}|| \times cos(\vec{u}, \vec{u}) $$
Mais \(cos(\vec{u}, \vec{u}) = cos \left(0\right) = 1 \).
Alors, il reste uniquement les normes des deux vecteurs.
Soit finalement :
$$ \forall \vec{u},$$
$$ \vec{u}.\vec{u} = || \vec{u} ||^2 $$
Soient \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}\) et \(\vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) deux vecteurs dans un repère orthonormé \( (O, \vec{i}, \vec{j}, \vec{k})\) et telle que la figure suivante :
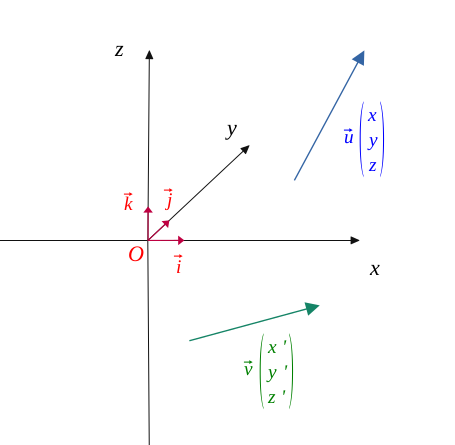
Alors on peut exprimer \(\vec{u} \) et \(\vec{v} \) sous la forme suivante :
$$ \Biggl \{ \begin{align*} \vec{u} = x \vec{i} + y \vec{j} +z \vec{k} \\ \vec{v} = x' \vec{i} + y' \vec{j} +z' \vec{k} \end{align*} $$
Alors le produit scalaire \(\vec{u}.\vec{v} \) vaut :
$$ \vec{u}.\vec{v} = (x \vec{i} + y \vec{j} +z \vec{k}) . ( x' \vec{i} + y' \vec{j} +z' \vec{k}) $$
$$ \vec{u}.\vec{v} = xx'\vec{i}.\vec{i} + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yy''\vec{j}.\vec{j} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} + zz'\vec{k}.\vec{k} $$
$$ \vec{u}.\vec{v} = xx' || \vec{i} ||^2 + yy''|| \vec{j} ||^2 + zz'|| \vec{k} ||^2 + xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} \qquad (1) $$
Les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont par hypothèse nos vecteurs unitaires, alors :
$$ || \vec{i} ||^2 = || \vec{j} ||^2 = || \vec{k} ||^2 = 1 $$
Par ailleurs, étant dans un repère orthonormaux, les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont orthogonaux, alors leur produit scalaire est nul :
$$ \vec{i}.\vec{j} = \vec{i}.\vec{k}= \vec{j}.\vec{k} = 0 $$
Et par commutativité du produit scalaire, on a aussi :
$$ \vec{j}.\vec{i} = \vec{k}.\vec{i}= \vec{k}.\vec{j} = 0 $$
Soit en réécrivant \((1) \),
$$ \vec{u}.\vec{v} = xx' + yy'' + zz' + \hspace{0.1em} \underbrace { xy'\vec{i}.\vec{j} + xz'\vec{i}.\vec{k} + yx'\vec{j}.\vec{i} + yz'\vec{j}.\vec{k} + zx'\vec{k}.\vec{i} + zy'\vec{k}.\vec{j} } _\text{ \(= \hspace{0.1em} 0\)} $$
Et finalement,
$$ \forall \left [\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix} , \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix} \right], $$
$$ \vec{u}. \vec{v} = xx' + yy' +zz' $$
Soient \((\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2\) deux réels et \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}, \ \vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) deux vecteurs.
En effectuant le produit scalaire \( (\lambda\vec{u}).\vec{v}\), on a :
$$ (\lambda\vec{u}).\vec{v} = || \lambda \vec{u} || \times || \vec{v} || \times cos(\lambda \vec{u}, \vec{v}) $$
La norme \( || \lambda \vec{u} || \) du vecteur \( \vec{\lambda u}\begin{pmatrix} \lambda x\\ \lambda y\\ \lambda z \end{pmatrix} \) vaut :
$$ || \lambda \vec{u} || = \sqrt{ (\lambda x)^2 + (\lambda y)^2 + (\lambda z)^2 }$$
$$ || \lambda \vec{u} || = \sqrt{ \lambda^2 (x^2 + y^2 + z^2) }$$
$$ || \lambda \vec{u} || = |\lambda| \times || \vec{u} ||$$
Soit,
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times || \vec{u} || \times || \vec{v} || \times cos(\lambda \vec{u}, \vec{v}) $$
Concernant l'angle \( (\lambda \vec{u}, \vec{v}) \), il n'est pas différent de \( ( \vec{u}, \vec{v}) \), car \( ( \lambda \vec{u}) \) n'est que le prolongement du vecteur \( \vec{u}\).
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times || \vec{u} || \times || \vec{v} || \times cos( \vec{u}, \vec{v}) $$
Soit finalement,
$$ \forall \lambda \in \hspace{0.05em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = |\lambda| \times \vec{u}. \vec{v}$$
Par ailleurs, en effectuant le même raisonnement, on obtient aussi la linéarité à droite :
$$ \forall \lambda \in \hspace{0.05em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
On a alors une bilinéarité :
$$ \forall \lambda \in \hspace{0.05em} \mathbb{R}, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).\vec{v} = \vec{u}.(\lambda\vec{v}) = |\lambda| \times \vec{u}. \vec{v}$$
Par ailleurs, en effectuant le produit scalaire \( (\lambda\vec{u}).(\mu\vec{v})\), on obtient :
$$ \forall (\lambda, \mu) \in \hspace{0.05em} \mathbb{R}^2, \ \forall (\vec{u}, \vec{v}),$$
$$ (\lambda\vec{u}).(\mu\vec{v}) = |\lambda| \times |\mu| \times \vec{u}. \vec{v} $$
Soient \(\vec{u}\begin{pmatrix} x\\ y\\z \end{pmatrix}\), \(\vec{v}\begin{pmatrix} x'\\ y'\\z' \end{pmatrix}\) et \(\vec{w}\begin{pmatrix} x''\\ y''\\z'' \end{pmatrix}\) trois vecteurs.
On exprime les vecteurs \(\vec{u} \), \(\vec{v} \) et \(\vec{w} \) sous la forme suivante :
$$ \left \{ \begin{align*} \vec{u} = x \vec{i} + y \vec{j} +z \vec{k} \\ \vec{v} = x' \vec{i} + y' \vec{j} +z' \vec{k} \\ \vec{w} = x'' \vec{i} + y'' \vec{j} +z'' \vec{k} \end{align*} \right \} $$
Alors le produit scalaire \(\vec{u}.( \vec{v} + \vec{w}) \) vaut :
$$ \vec{u}.( \vec{v} + \vec{w}) = (x \vec{i} + y \vec{j} +z \vec{k}) . ( x' \vec{i} + y' \vec{j} +z' \vec{k} + x'' \vec{i} + y'' \vec{j} +z'' \vec{k}) $$
$$ \vec{u}.( \vec{v} + \vec{w}) = (x \vec{i} + y \vec{j} +z \vec{k}) . \Bigl( (x' + x'') \vec{i} + (y' + y'') \vec{j} + (z' + z'') \vec{k} \Bigr) $$
$$ \vec{u}.( \vec{v} + \vec{w}) = (x(x' + x'')) \vec{i}.\vec{i} + (x(y' + y'')) \vec{i}.\vec{j} + (x(z' + z'')) \vec{i}.\vec{k} + (y(x' + x'')) \vec{j}.\vec{i} + (y(y' + y'')) \vec{j}.\vec{j} + (y(z' + z'')) \vec{j}.\vec{k} + (z(x' + x'')) \vec{k}.\vec{i} + (z(y' + y'')) \vec{k}.\vec{j} + (z(z' + z'')) \vec{k}.\vec{k} $$
$$ \vec{u}.( \vec{v} + \vec{w}) = (x(x' + x'')) ||\vec{i}||^2 + (y(y' + y'')) ||\vec{j}||^2 + (z(z' + z'')) ||\vec{k}||^2 + (x(y' + y'')) \vec{i}.\vec{j} + (y(x' + x''))+ \vec{j}.\vec{i} + (y(z' + z'')) \vec{j}.\vec{k} + (z(x' + x'')) \vec{k}.\vec{i} + (z(y' + y'')) \vec{k}.\vec{j} + (x(z' + z'')) \vec{i}.\vec{k} \qquad(2) $$
Les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont par hypothèse nos vecteurs unitaires, alors :
$$ || \vec{i} ||^2 = || \vec{j} ||^2 = || \vec{k} ||^2 = 1 $$
Par ailleurs, étant dans un repère orthonormaux, les trois vecteurs \(\vec{i},\vec{j}, \vec{k} \) sont orthogonaux, alors leur produit scalaire est nul :
$$ \vec{i}.\vec{j} = \vec{i}.\vec{k}= \vec{j}.\vec{k} = 0 $$
Et par commutativité du produit scalaire, on a aussi :
$$ \vec{j}.\vec{i} = \vec{k}.\vec{i}= \vec{k}.\vec{j} = 0 $$
Soit en réécrivant \((2) \),
$$ \vec{u}.( \vec{v} + \vec{w}) = (x(x' + x'')) + (y(y' + y'')) + (z(z' + z'')) + \hspace{0.1em} \underbrace{ (x(y' + y'')) \vec{i}.\vec{j} + (y(x' + x''))+ \vec{j}.\vec{i} + (y(z' + z'')) \vec{j}.\vec{k} + (z(x' + x'')) \vec{k}.\vec{i} + (z(y' + y'')) \vec{k}.\vec{j} + (x(z' + z'')) \vec{i}.\vec{k} } _\text{ \(= \hspace{0.1em} 0\)} $$
$$ \vec{u}.( \vec{v} + \vec{w}) = (x(x' + x'')) + (y(y' + y'')) + (z(z' + z'')) $$
$$ \vec{u}.( \vec{v} + \vec{w}) = xx' + xx'' + yy' + yy'' + zz' + zz'' \qquad (3) $$
En réarrangent l'expression \( (3) \) :
$$ \vec{u}.( \vec{v} + \vec{w}) = xx' + yy' + zz' + xx'' + yy'' + zz'' $$
On reconnaît l'écriture de \( \vec{u}.\vec{v} \) et \( \vec{u}.\vec{w} \) sous la forme du Produit des coordonnées :
$$ \vec{u}.( \vec{v} + \vec{w}) = \hspace{0.1em} \underbrace { xx' + yy' + zz' } _\text{ \(= \hspace{0.1em} \vec{u}.\vec{v} \)} \hspace{0.1em} + \hspace{0.1em} \underbrace { xx'' + yy'' + zz'' } _\text{ \(= \hspace{0.1em} \vec{u}.\vec{w} \)} $$
Soit finalement,
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ \vec{u}.( \vec{v} + \vec{w}) = \vec{u}.\vec{v} + \vec{u}.\vec{w} $$
Et grâce à la commutativité du produit scalaire, on a aussi la distributivité à gauche :
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{w} . (\vec{u} + \vec{v}) $$
En développant l'expression avec la distributivité à droite, on a :
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
Soit finalement,
$$ \forall (\vec{u}, \vec{v}, \vec{w}), $$
$$ (\vec{u} + \vec{v}) . \vec{w} = \vec{u}.\vec{w} + \vec{v}.\vec{w} $$
On a vu plus haut que le produit scalaire est distributif, c'est la propriété qui va être utilisée dans cette partie.
$$ (\vec{u} + \vec{v})^2 = (\vec{u} + \vec{v}).(\vec{u} + \vec{v}) $$
$$ (\vec{u} + \vec{v})^2 =\vec{u}. \vec{u} + \vec{u}.\vec{v} + \vec{u}.\vec{v} - \vec{v}. \vec{v} $$
$$ (\vec{u} + \vec{v})^2 = || \vec{u} ||^2 + 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
C'est la même chose avec un signe \((-)\) dans le double produit.
$$ (\vec{u} \textcolor{#A65757}{-} \vec{v})^2 = (\vec{u} \textcolor{#A65757}{-} \vec{v}).(\vec{u} \textcolor{#A65757}{-} \vec{v}) $$
$$ (\vec{u} \textcolor{#A65757}{-} \vec{v})^2 =\vec{u}. \vec{u} \textcolor{#A65757}{-} \vec{u}.\vec{v} \textcolor{#A65757}{-} \vec{u}.\vec{v} - \vec{v}. \vec{v} $$
$$ (\vec{u} \textcolor{#A65757}{-} \vec{v})^2 = || \vec{u} ||^2 \textcolor{#A65757}{-} 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
$$ (\vec{u} + \vec{v}). (\vec{u} - \vec{v}) = \vec{u}. \vec{u} - \vec{u}. \vec{v} + \vec{v}. \vec{u} - \vec{v}. \vec{v} $$
On a vu que le produit scalaire est commutatif, alors \( \vec{u}. \vec{v} = \vec{v}. \vec{u} \), et :
$$ (\vec{u} + \vec{v}). (\vec{u} - \vec{v}) = || \vec{u} ||^2 \hspace{0.1em} \underbrace{ - \ \vec{u}. \vec{v} + \vec{u}. \vec{v} } _\text{ \(= \hspace{0.1em} 0 \)} \hspace{0.1em} - || \vec{v} ||^2$$
$$ || \vec{u} ||^2 - || \vec{v} ||^2= (\vec{u} + \vec{v}) (\vec{u} - \vec{v}) $$
On obtient exactement les mêmes formules que les identités remarquables classiques.
On a vu plus que :
$$ \Biggl \{ \begin{align*} (\vec{u} + \vec{v})^2 = || \vec{u} ||^2 + 2 \vec{u}.\vec{v} + || \vec{v} ||^2 \qquad (4) \\ (\vec{u} - \vec{v})^2 = || \vec{u} ||^2 - 2 \vec{u}.\vec{v} + || \vec{v} ||^2 \qquad (5) \end{align*} $$
En travaillant avec l'expression \( (4) \), on a :
$$ (\vec{u} + \vec{v})^2 = || \vec{u} ||^2 + 2 \vec{u}.\vec{v} + || \vec{v} ||^2 \qquad (4) $$
Mais grâce à la propriété des carrés scalaires, on sait que :
$$ \forall \vec{u}, \ (\vec{u})^2 = || \vec{u} ||^2 $$
Alors l'expression \( (4) \) devient :
$$ || \vec{u} + \vec{v} ||^2 = || \vec{u} ||^2 + 2 \vec{u}.\vec{v} + || \vec{v} ||^2$$
$$2 \vec{u}.\vec{v} = || \vec{u} + \vec{v} ||^2 - || \vec{u} ||^2 - || \vec{v} ||^2$$
Et finalement,
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( || \vec{u} + \vec{v} ||^2 - || \vec{u} ||^2 - || \vec{v} ||^2 \right ) $$
De la même manière, avec l'expression \( (5) \), on a :
$$ (\vec{u} \textcolor{#A65757}{-} \vec{v})^2 = || \vec{u} ||^2 \textcolor{#A65757}{-} 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
$$ ||\vec{u} - \vec{v}||^2 = || \vec{u} ||^2 - 2 \vec{u}.\vec{v} + || \vec{v} ||^2 $$
$$ 2 \vec{u}.\vec{v} = || \vec{u} ||^2 + || \vec{v} ||^2 - ||\vec{u} - \vec{v}||^2 $$
$$ \vec{u}.\vec{v} =\frac{1}{2} \left( || \vec{u} ||^2 + || \vec{v} ||^2 - || \vec{u} -\vec{v} ||^2 \right ) $$
Soit un plan \((\mathcal{P})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et orthogonal à un vecteur \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\)(avec \(a, b, c \) non nuls tous les trois).
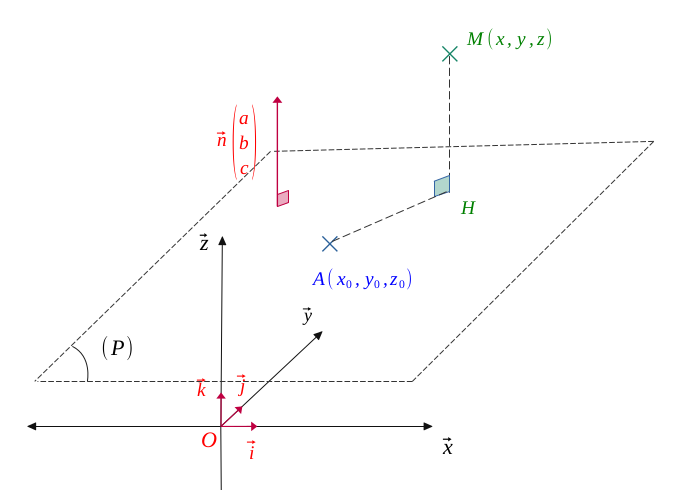
Il s'agit de déterminer la distance \([HM]\) du point \(M(x, y, z)\) au plan \((\mathcal{P})\).
Comme les vecteurs \(\vec{n}\) et \(\overrightarrow{HA}\) sont orthogonaux, on a :
$$ \vec{n} \ . \ \overrightarrow{HA} = 0$$
$$ \vec{n} \ . \ (\overrightarrow{HM} + \ \overrightarrow{MA}) = 0$$
$$ \vec{n} \ . \ \overrightarrow{HM} + \ \vec{n} \ . \ \overrightarrow{MA} = 0$$
$$ || \vec{n} || \times || \overrightarrow{HM} || + \vec{n} \ . \ \overrightarrow{MA} = 0$$
$$ || \overrightarrow{HM} || = \frac{\vec{n} \ . \ \overrightarrow{AM}}{ || \vec{n} ||} $$
$$ HM = \left | \frac{\vec{n} \ . \ \overrightarrow{AM}}{ || \vec{n} ||} \right| $$
Alors, connaissant les coordonnées du point \(M\), on peut appliquer la méthode de calcul du produit scalaire par le produit des coordonnées :
$$ HM = \left | \frac{a(x -x_0) + b(y-y_0) + c(z-z_0) }{ \sqrt{a^2 + b^2 + c^2}} \right| $$
 Retour en haut de page
Retour en haut de page