








Soient \((p,n) \in \hspace{0.05em}\mathbb{N}^2 \) deux entiers naturels avec \( p \leqslant n \).
On appelle \(\binom{n}{p} \) ("\( p \) parmis \( n \)") le nombre de façons de prendre \( p \) éléments parmis \( n \) éléments d'un ensemble.
On l'appelle aussi le binôme, il répond à la formule suivante :
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n!}{p!(n-p)!} $$
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{0} = \binom{n}{n} = 1$$
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{1} = n$$
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \binom{n}{n-p} $$
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n - 1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad (Pascal) $$
$$\forall n \in \mathbb{N}, $$
$$ \sum_{p = 0}^n \binom{n}{p} = \hspace{0.2em} 2^n $$
$$\forall (r, n) \in \hspace{0.05em}\mathbb{N}^2, \enspace r \leqslant n, $$
$$ \sum_{k=r}^n \binom{k}{r} = \binom{n+1}{r +1} $$
Récapitulatif des propriétés du binôme
Soient \((p,n) \in \hspace{0.05em}\mathbb{N}^2 \) deux entiers naturels avec \( p \leqslant n \).
Il n'existe qu'une seule manière de prendre aucun ou tous les éléments d'un ensemble composé de \( n \) éléments.
Autrement, par la formule du binôme, on a :
$$ \binom{n}{0} = \frac{n!}{0! \ n!} =1 $$
Idem avec \(n\), on a :
$$ \binom{n}{n} = \frac{n!}{ n! \ 0! } =1 $$
Soit finalement,
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{0} = \binom{n}{n} = 1$$
Par la formule du binôme, on a :
$$ \binom{n}{1} = \frac{n!}{1! \ (n-1)!} =1 $$
$$ \binom{n}{1} = \frac{n (n-1)!}{1! \ (n-1)!} = n $$
Soit finalement,
$$ \forall n \in \mathbb{N}, $$
$$ \binom{n}{1} = n$$
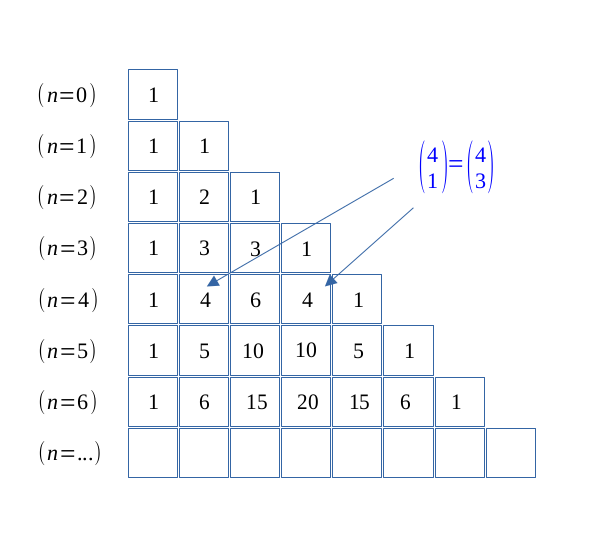
Le triangle de Pascal illustre bien la symétrie qu'il y a entre les \( p\) et \( (n-p) \) éléments pris parmis \(n\).

Par ailleurs, on peut voir par le calcul que :
$$ \binom{n}{p} = \frac{n!}{p!(n-p)!} $$
$$ \binom{n}{n-p} = \frac{n!}{ (n-p)! (n - (n-p))!} = \frac{n!}{p!(n-p)!}$$
Soit,
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \binom{n}{n-p} $$
Par la formule du binôme, on a :
$$ \binom{n}{p} = \frac{n!}{p!(n-p)!} $$
$$ \binom{n}{p} = \frac{n(n-1)!}{p(p-1)!(n-p)!} $$
$$ \binom{n}{p} = \frac{n}{p} \frac{(n-1)!}{(p-1)!(n-p)!} $$
Or, on remarque qu'au dénominateur :
$$ n-p = (n-1) - (p-1) $$
Alors,
$$ \binom{n}{p} = \frac{n}{p} \frac{(n-1)!}{(p-1)!((n-1) - (p-1))!} $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
Soit,
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n, $$
$$ \binom{n}{p} = \frac{n}{p} \binom{n -1}{p-1} $$
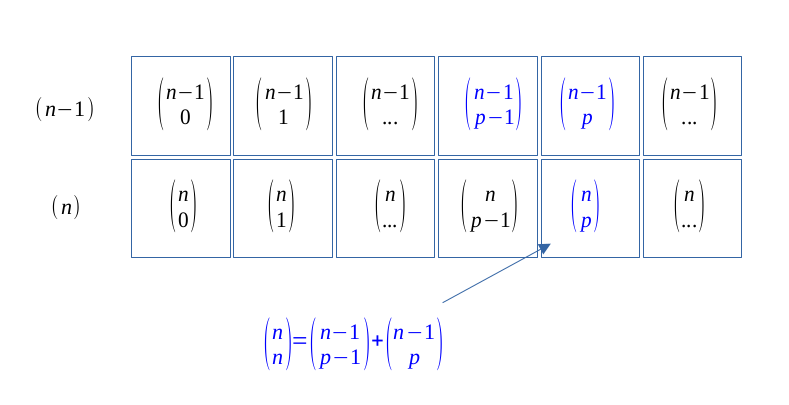
Pour retrouver le triangle de Pascal, on additionne une case avec son voisin de gauche pour trouver le voisin du dessous.
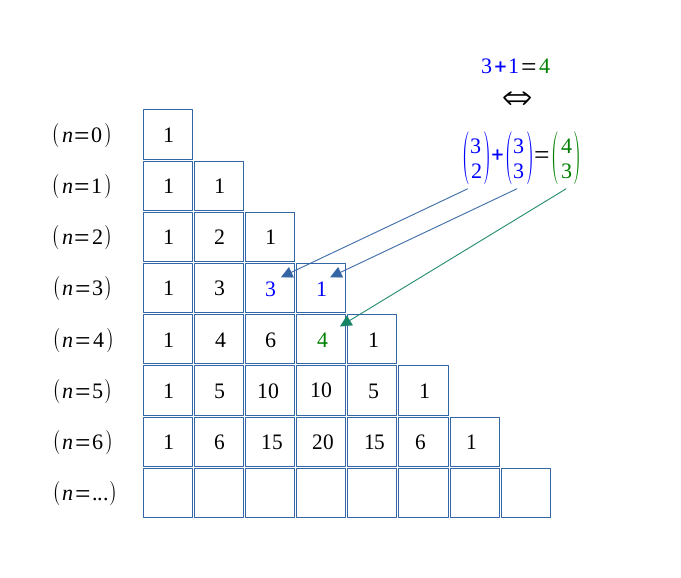
Par ailleurs, si l'on considère les rangs \( (n-1)\) et \(n\) du Le triangle de Pascal, la formule apparaît clairement.

Par visualisation il est évident que,
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad (Pascal) $$
Considérons un ensemble \( E \) comprenant \(n\) éléments.
$$ E = \Bigl \{ e_1, e_2 , \hspace{0.2em} ... \hspace{0.2em}, e_{n} \Bigr\} $$
Dans cet ensemble, le nombre de parties possibles contenant \( p \) éléments est \( \binom{n}{p} \).
Séparons cet ensemble en deux ensembles distincts : \( E_1 \) et \( E_2 \).
$$ E_1 = \begin{Bmatrix} \Bigl \{ e_1 , e_2, e_3, \ ... \ , e_n \Bigr \} \\ \Bigl\{ e_1 , e_3, e_4, \ ... \ , e_n \Bigr \} \\ \Bigl\{ e_1 , e_2, e_4, \ ... \ , e_n \Bigr \} \\ \Bigl\{................ \Bigr \} \\ \Bigl \{ \underbrace { e_1 , e_2, e_4, \ ... \ , e_n} _\text{ \(p\) éléments } \Bigr \} \\ \end{Bmatrix} $$
Étant donné que toutes ces parties contiennent \( e_n \), cela simplifie l'ensemble \( E_1 \) :
$$ E_1 = \begin{Bmatrix} \Bigl \{ e_1 , e_2, e_3, \ ... \ , e_n \Bigr \} \\ \Bigl\{ e_1 , e_3, e_4, \ ... \ , e_n \Bigr \} \\ \Bigl\{ e_1 , e_2, e_4, \ ... \ , e_n \Bigr \} \\ \Bigl\{................ \Bigr \} \\ \Bigl \{ \underbrace { e_1 , e_2, e_4, \ ... \ , e_n} _\text{ \(p\) éléments } \Bigr \} \\ \end{Bmatrix} \enspace \Longrightarrow \enspace \begin{Bmatrix} \Bigl \{ e_1 , e_2, e_3, \ ... \ \Bigr \} \\ \Bigl\{ e_1 , e_3, e_4, \ ... \ \Bigr \} \\ \Bigl\{ e_1 , e_2, e_4, \ ... \ \Bigr \} \\ \Bigl\{............. \Bigr \} \\ \Bigl \{ \underbrace { e_1 , e_2, e_4, \ .... } _\text{ \((p -1)\) éléments } \Bigr \} \\ \end{Bmatrix} $$
Alors le nombre d'éléments de \( E_1 \) se réduira au nombre de façons de prendre \( (p -1) \) éléments parmis \( (n-1) \) éléments dans \( E\), c'est-à-dire \( \binom{n -1}{p -1} \).
$$ E_2 = \underbrace { \begin{Bmatrix} { e_1 , e_2, e_3, \ ... } \\ { e_1 , e_3, e_4, \ ... } \\ { e_1 , e_2, e_4, \ ... } \\ {............. } \\ { e_1 , e_2, e_4, \ ... } \\ \end{Bmatrix} } _\text{ \(p\) éléments } $$
Comme \( E_2 \) ne contient pas \(e_n\), alors il restera un choix de \( (n-1) \) éléments pour en prendre \( p \). C'est-à-dire \( \binom{n -1}{p} \).
On a alors montré que :
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad (Pascal) $$
Calculons \( \binom{n -1}{p -1} + \binom{n -1}{p} \) :
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) !}{ p! \ (n-1-p)!} + \frac{(n-1) !}{ (p-1)! \ (n-1-(p-1))!} $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) !}{ p! \ (n-1-p)!} + \frac{(n-1) !}{ (p-1)! \ (n-p)!} $$
On met ces deux termes au même dénominateur :
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ \textcolor{#A65757}{(n-p)}}{ p! \ (n-1-p)! \ \textcolor{#A65757}{(n-p)}} + \frac{(n-1) ! \ \textcolor{#A65757}{p}}{ (p-1)! \ (n-p)! \ \textcolor{#A65757}{p}} $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ (n-p)}{ p! (n-p)! } + \frac{(n-1) ! \ p }{ p! \ (n-p)!} $$
Et on factorise :
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{(n-1) ! \ (n-p + p)}{ p! (n-p)! } $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \frac{n!}{ p! (n-p)! } $$
$$ \binom{n -1}{p -1} + \binom{n -1}{p} = \binom{n}{p} $$
On a alors montré que,
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n -1}{p -1 } + \binom{n - 1}{p} \qquad (Pascal) $$
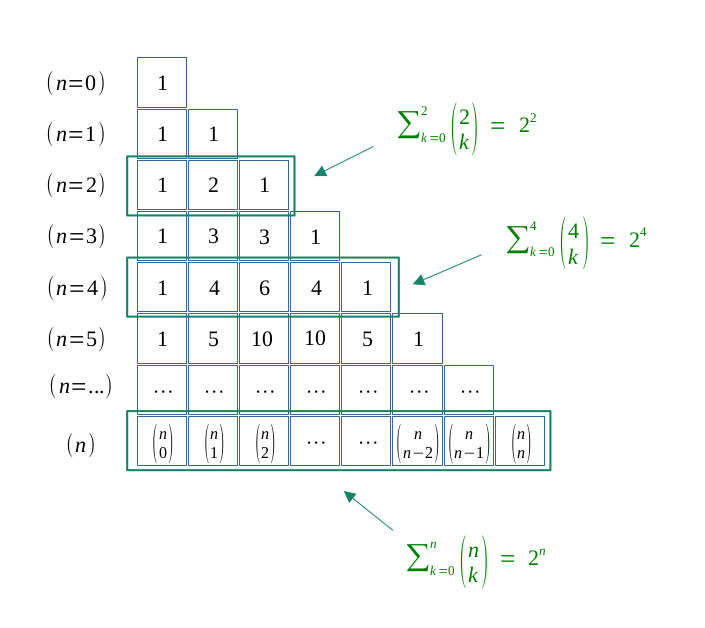
Soit \( n \in \mathbb{N}\) un entier naturel.
On souhaite calculer la somme horizontale des \( \binom{n}{k} \), de \( 0\) jusqu'à \( n\).
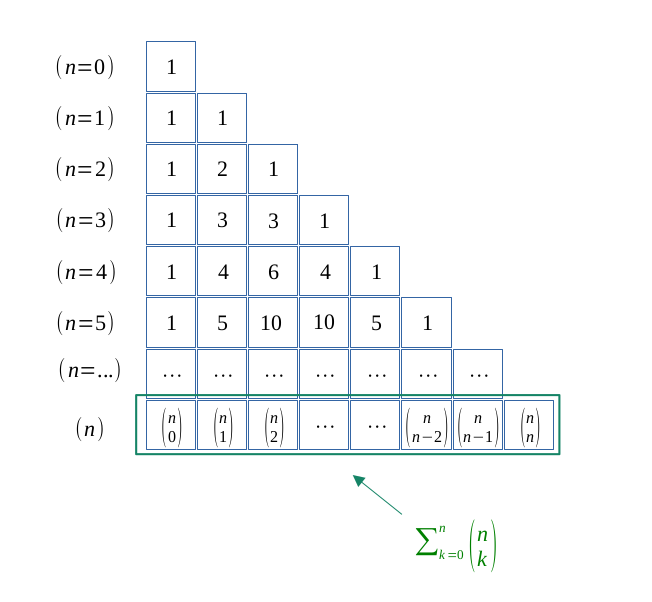
Le binôme de Newton nous dit que :
$$\forall n \in \mathbb{N}, \enspace \forall (a, b) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ (a + b)^n = \sum_{p = 0}^n \binom{n}{p} a^{n-p}b^p $$
En prenant \( \{ a = 1, \enspace b = 1 \}\), on a :
$$ (1 + 1)^n = \sum_{p = 0}^n \binom{n}{p} $$
Et finalement,
$$\forall n \in \mathbb{N}, $$
$$ 2^n = \sum_{p = 0}^n \binom{n}{p} $$
Soit :
$$ 2^n \hspace{0.2em} = \binom{n}{0} + \binom{n}{1} \enspace + ... + \enspace \binom{n}{n-1} + \binom{n}{n} $$
Essayons de montrer que la proposition suivante \((P_n)\) est vraie :
$$\forall n \in \mathbb{N}, $$
$$ 2^n \hspace{0.2em} = \binom{n}{0} + \binom{n}{1} \enspace + ... + \enspace \binom{n}{n-1} + \binom{n}{n} \qquad (P_n) $$
Vérifions que c'est bien vrai pour le premier terme, c'est-à-dire lorsque \( n = 0 \).
$$ \sum_{p = 0}^0 \binom{0}{p} = \binom{0}{0} = 1 $$
Or,
$$ 2^0 = 1 $$
On a donc bien :
$$ 2^0 \hspace{0.2em} = \sum_{p = 0}^0 \binom{0}{p} $$
\((P_0)\) est vraie.
Soit \( k \in \mathbb{N} \) un entier naturel.
On suppose que la proposition \((P_k)\) est vraie pour tout \( k \).
$$ 2^{k} \hspace{0.2em} = \binom{k}{0} + \binom{k}{1} \enspace + ... + \enspace \binom{k}{k} + \binom{k}{k} \qquad (P_{k}) $$
Vérifions que c'est bien le cas pour \((P_{k + 1})\).
$$ 2^{k + 1} \hspace{0.2em} = \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} \qquad (P_{k + 1}) $$
Calculons le membre de droite de \(( P_{k + 1} ) \):
$$ \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} $$
Mais on sait grâce à la formule de Pascal, que :
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n - 1}{p - 1} + \binom{n - 1}{p} \qquad (Pascal) $$
Soit aussi que :
$$ \binom{n + 1}{p + 1} = \binom{n}{p} + \binom{n}{p + 1} \qquad (Pascal^*) $$
$$ \textcolor{#606B9E}{\binom{k + 1}{0}} + \textcolor{#446e4f}{\binom{k + 1}{1}} + \textcolor{#A65757}{ \binom{k + 1}{2}} \enspace + ... + \enspace \textcolor{#7C578A}{\binom{k + 1}{k}} + \textcolor{#606B9E}{\binom{k + 1}{k + 1}} $$
Alors grâce à \( (Pascal^*)\), on a :
$$ \textcolor{#606B9E}{\binom{k + 1}{0}} + \textcolor{#446e4f}{\binom{k}{0} + \binom{k}{1}} + \textcolor{#A65757}{\binom{k}{1} + \binom{k}{2}} \enspace + ... + \enspace \textcolor{#7C578A}{\binom{k}{k - 1} + \binom{k}{k}} + \textcolor{#606B9E}{\binom{k + 1}{k + 1}} $$
Or, le premier terme est égal au second.
$$ \binom{k + 1}{0} = \binom{k}{0} $$
De même, le dernier est égal à l'avant-dernier.
$$ \binom{k + 1}{k + 1} = \binom{k}{k} $$
Ce qui nous amène à :
$$ \binom{k}{0} + \binom{k}{0} + \binom{k}{1} + \binom{k}{1} + \binom{k}{2} \enspace + ... + \enspace \binom{k}{k - 1} + \binom{k}{k} +\binom{k}{k} $$
Puis finalement :
$$ 2 \left[ \binom{k}{0} + \binom{k}{1} + \binom{k}{2} \enspace + ... + \enspace \binom{k}{k - 1} + \binom{k}{k} \right] $$
Or, notre hypothèse était que :
$$ 2^k \hspace{0.2em} = \binom{k}{0} + \binom{k}{1} \enspace + ... + \enspace \binom{k}{k-1} + \binom{k}{k} \qquad (P_k) $$
On en déduit que :
$$ 2 \times 2^{k} \hspace{0.2em} = \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} $$
Soit :
$$ 2^{k + 1} \hspace{0.2em} = \binom{k + 1}{0} + \binom{k + 1}{1} \enspace + ... + \enspace \binom{k + 1}{k} + \binom{k + 1}{k + 1} \qquad (P_{k+1}) $$
\((P_{k + 1})\) est vraie.
La proposition \((P_n)\) est vraie pour son premier terme \(n_0 = 0\) et est héréditaire de proche en proche pour tout \(k \in \mathbb{N}\).
Par le principe de récurrence, elle ainsi est vraie pour tout \(n \in \mathbb{N}\).
Nous venons de prouver par une récurrence que :
$$\forall n \in \mathbb{N}, $$
$$ 2^n \hspace{0.2em} = \sum_{p = 0}^n \binom{n}{p} $$

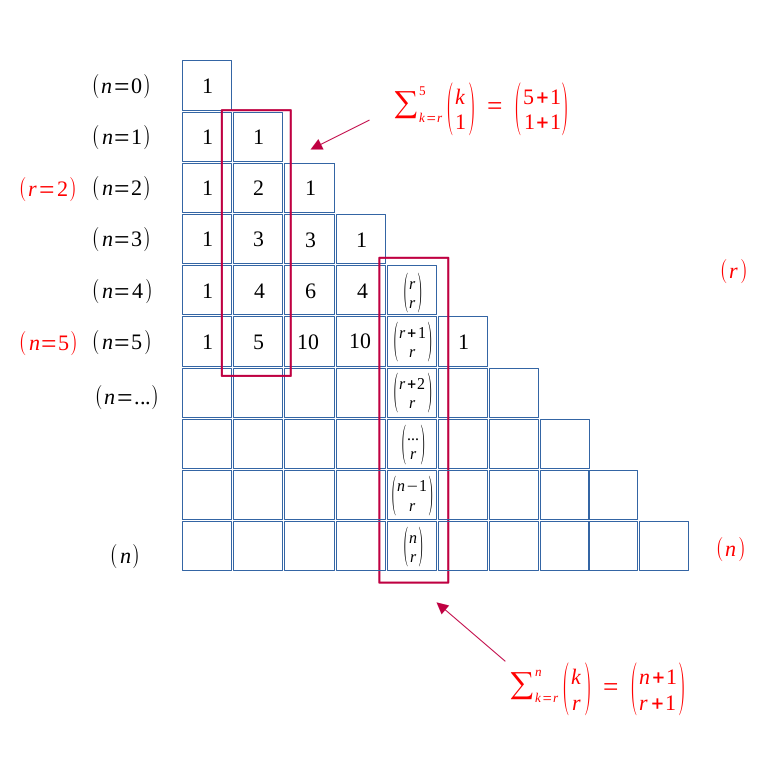
Soit \( (r, n) \in \hspace{0.05em} \mathbb{N}^2\) deux entiers naturels.
On souhaite calculer la somme verticale des \( \binom{k}{r} \), de \( r\) jusqu'à \( n\).
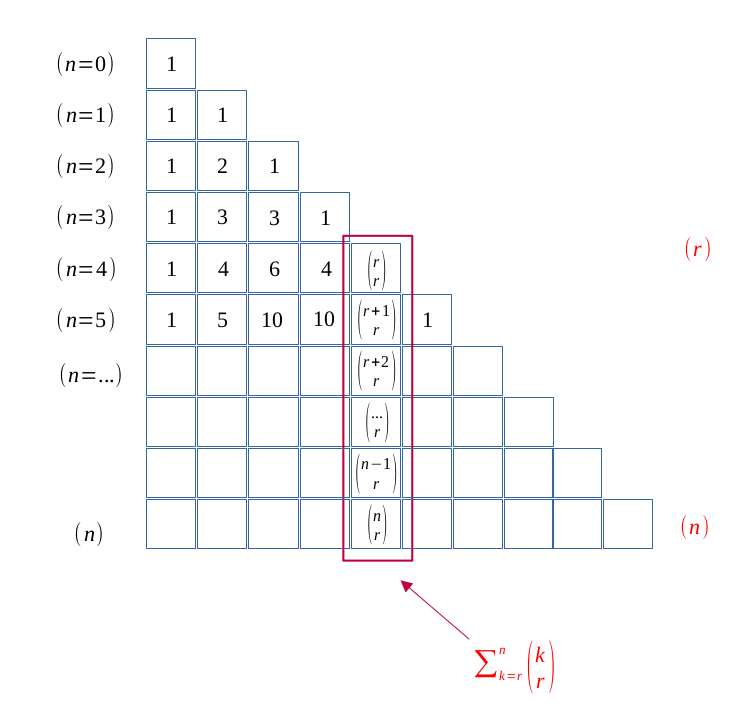
On sait par la formule de Pascal, que :
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n - 1}{p - 1} + \binom{n - 1}{p} \qquad (Pascal) $$
Soit aussi que :
$$ \binom{n + 1}{p + 1} = \binom{n}{p} + \binom{n}{p + 1} \qquad (Pascal^*) $$
Soit, en remplaçant dans notre cas,
$$ \forall (r,k) \in \hspace{0.05em}\mathbb{N}^2, \enspace r +1 \leqslant k, \enspace \binom{k + 1}{r + 1} = \binom{k}{r} + \binom{k}{r + 1} $$
Et,
$$ \binom{k}{r} = \binom{k + 1}{r + 1} - \binom{k}{r + 1} \qquad (1) $$
En extractant le premier terme de la somme recherchée :
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \sum_{k=r + 1}^n \binom{k}{r} $$
On injecte à présent \((1) \) :
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \sum_{k=r + 1}^n \Biggl[ \binom{k + 1}{r + 1} - \binom{k}{r + 1} \Biggr] $$
On voit ici que la somme du membre de droite est une somme téléscopique, on a alors en simplifiant :
$$ \sum_{k=r}^n \binom{k}{r} = \binom{r}{r} + \binom{n + 1}{r + 1} - \binom{r+1}{r + 1} $$
$$ \sum_{k=r}^n \binom{k}{r} = 1 + \binom{n + 1}{r + 1} - 1 $$
Et finalement,
$$\forall (r, n) \in \hspace{0.05em}\mathbb{N}^2, \enspace r \leqslant n, $$
$$ \sum_{k=r}^n \binom{k}{r} = \binom{n+1}{r +1} $$

 Retour en haut de page
Retour en haut de page