








Le binôme de Newton nous dit que :
$$\forall n \in \mathbb{N}, \enspace \forall (a, b) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ (a + b)^n = \sum_{p = 0}^n \binom{n}{p} a^{n-p}b^p \qquad (Newton ) $$
On peut utiliser le triangle de Pascal pour trouver les coefficients binomiaux \(\binom{n}{p}\).
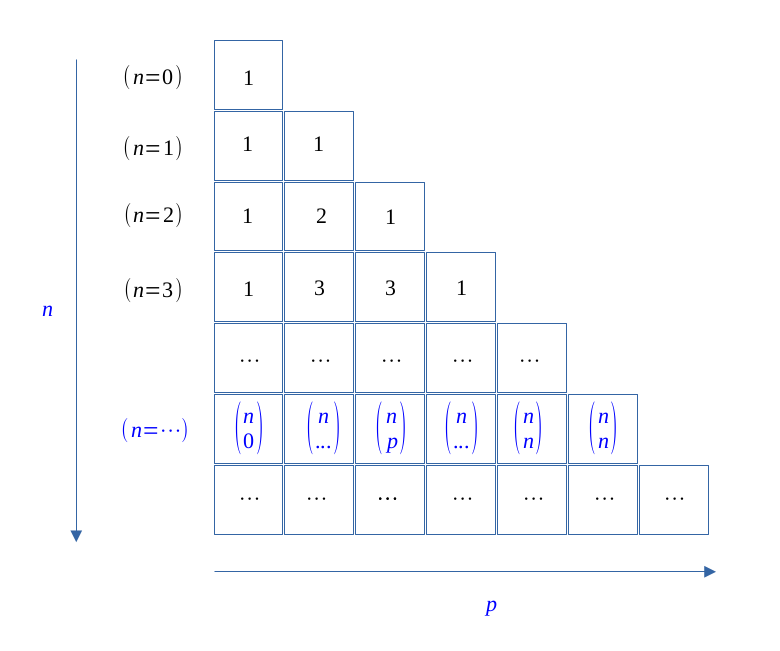
$$ (a + b)^n = a^n + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b \hspace{0.1em} + \hspace{0.1em} \dots \hspace{0.1em} + \binom{n}{n-2}ab^{n-2} + \binom{n}{n-1}ab^{n-1} +b^n $$
Montrons par une récurrence que la proposition suivante \((P_n)\) est vraie :
$$\forall n \in \mathbb{N}, \enspace \forall (a, b) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ (a + b)^n = \sum_{p = 0}^n \binom{n}{p} a^{n-p}b^p \qquad (P_n) $$
Vérifions que c'est bien vrai pour le premier terme, c'est-à-dire lorsque \( n = 0 \).
$$ \sum_{p = 0}^0 \binom{0}{p} a^{0-p}b^p = a^{0 - 0}b^0 = 1 $$
Or,
$$ (a + b)^0 = 1 $$
On a donc bien :
$$ (a + b)^0 = \sum_{p = 0}^0 \binom{0}{p} a^{0-p}b^p $$
\((P_0)\) est vraie.
Soit \( k \in \mathbb{N} \) un entier naturel.
On suppose que la proposition \((P_k)\) est vraie pour tout \( k \).
$$ (a + b)^{k} = \sum_{p = 0}^{k} \binom{k}{p} a^{k - p}b^p \qquad (P_{k}) $$
Vérifions que c'est bien le cas pour \((P_{k + 1})\).
$$ (a + b)^{k + 1} = \sum_{p = 0}^{k + 1} \binom{k + 1}{p} a^{k + 1 - p}b^p \qquad (P_{k + 1}) $$
Soit que :
$$ (a + b)^{k + 1} = \binom{k + 1}{0}a^{k + 1} + \binom{k + 1}{1}a^{k}b + \binom{k + 1}{2}a^{k-1}b^2 \ + \ ... \ + \ \binom{k + 1}{k}ab^{k} + \binom{k + 1}{k + 1}b^{k + 1} \qquad (P_{k + 1}') $$
Multiplions les membres de \(( P_{k} ) \) par \(( a + b) \).
$$ (a + b)^{k}(a + b) = (a + b) \times \sum_{p = 0}^k \binom{k}{p} a^{k-p}b^k $$
$$ (a + b)^{k + 1} = (a + b) \times \left[ \binom{k}{0}a^k + \binom{k}{1}a^{k - 1}b + \binom{k}{2}a^{k - 2}b^2 \ + \ ... \ + \ \binom{k}{k - 1}ab^{k -1} + \binom{k}{k} b^k \right] $$
$$ (a + b)^{k + 1} = \binom{k}{0} \left(a^{k + 1} + ba^k \right) + \binom{k}{1}\left(a^kb + a^{k - 1}b^2 \right) \ + \ ... \ + \ \enspace \binom{k}{k - 1}\left(a^2b^{k -1} + ab^k \right) + \binom{k}{k}\left(ab^k + b^{k + 1}\right) $$
$$ (a + b)^{k + 1} = \textcolor{#606B9E}{\binom{k}{0}} a^{k + 1} + \textcolor{#446e4f}{\left[\binom{k}{0} + \binom{k}{1} \right]} ba^k + \textcolor{#A65757}{\left[\binom{k}{1} + \binom{k}{2} \right]} a^{k - 1}b^2 \ + \ ... \ + \ \textcolor{#7C578A}{\left[\binom{k}{k -1} + \binom{k}{k} \right]}ab^k + \textcolor{#606B9E}{\binom{k}{k}} b^{k +1} $$
Mais on sait grâce à la formule de Pascal que :
$$ \forall (p,n) \in \hspace{0.05em}\mathbb{N}^2, \enspace p \leqslant n -1, $$
$$ \binom{n}{p} = \binom{n - 1}{p - 1} + \binom{n - 1}{p} \qquad (Pascal) $$
Soit aussi que :
$$ \binom{n + 1}{p + 1} = \binom{n}{p} + \binom{n}{p + 1} \qquad (Pascal^*) $$
Alors grâce à \( (Pascal^*) \), on a :
$$ (a + b)^{k + 1} = \textcolor{#606B9E}{\binom{k}{0}} a^{k + 1} + \textcolor{#446e4f}{\binom{k + 1}{1} } ba^k + \textcolor{#A65757}{\binom{k + 1}{2}} a^{k - 1}b^2 \ + \ ... \ + \ \textcolor{#7C578A}{\binom{k + 1}{k}}ab^k + \textcolor{#606B9E}{\binom{k}{k }} b^{k +1} $$
Or, on remarque que :
$$ \binom{k}{0} = \binom{k + 1}{0} $$
De même que :
$$ \binom{k}{k} = \binom{k + 1}{k + 1} $$
Et finalement que :
$$ (a + b)^{k + 1} = \binom{k + 1}{0} a^{k + 1} + \binom{k + 1}{1} ba^k + \binom{k + 1}{2} a^{k - 1}b^2 \ + \ ... \ + \ \binom{k + 1}{k}ab^k + \binom{k + 1}{k + 1 } b^{k +1} $$
On peut réécrire ce terme sous la forme de somme, et on retrouve bien notre proposition \(( P_{k + 1} ) \) :
$$ (a + b)^{k + 1} = \sum_{p = 0}^{k + 1} \binom{k + 1}{p} a^{k + 1 - p}b^p \qquad (P_{k + 1}) $$
\((P_{k + 1})\) est vraie.
La proposition \((P_n)\) est vraie pour son premier terme \(n_0 = 0\) et est héréditaire de proche en proche pour tout \(k \in \mathbb{N}\).
Par le principe de récurrence, elle ainsi est vraie pour tout \(n \in \mathbb{N}\).
Nous venons de prouver par une récurrence que :
$$\forall n \in \mathbb{N}, \enspace \forall (a, b) \in \hspace{0.05em} \mathbb{R}^2,$$
$$ (a + b)^n = \sum_{p = 0}^n \binom{n}{p} a^{n-p}b^p \qquad (Newton ) $$
 Retour en haut de page
Retour en haut de page