








Soit un répère orthonormé dans l'espace à trois dimensions \((O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\).
Équation paramétrique d'une droite
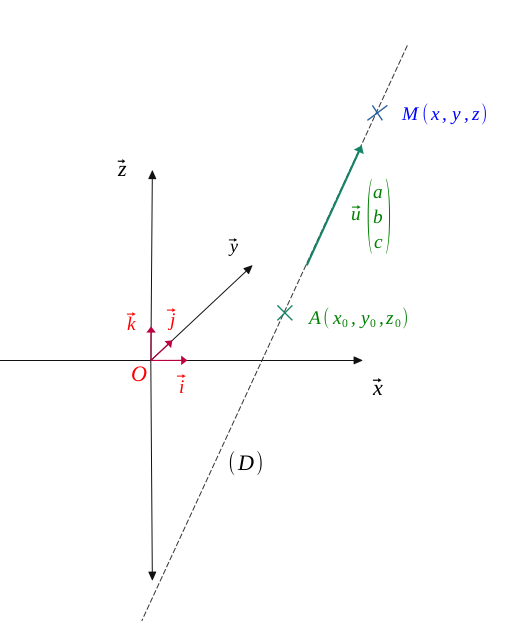
L'équation paramétrique d'une droite \(\mathcal{D}\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et dirigée par un vecteur \(\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix} \) (avec \(a, b, c \) non nuls tous les trois) est :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M(x, y, z) \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x = at + x_0 \\ y = bt + y_0 \\z = ct + z_0 \end{Bmatrix} $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \end{align*} $$
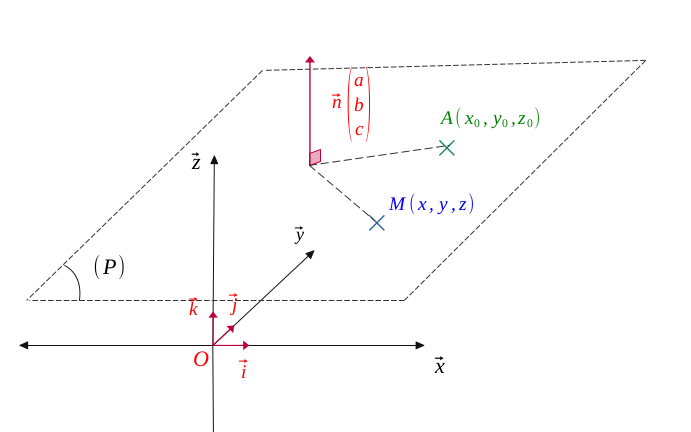
L'équation d'un plan \((\mathcal{P})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et orthogonal à un vecteur \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\) (avec \(a, b, c \) non nuls tous les trois) est :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M(x, y, z) \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} ax + by + cz + d = 0$$
$$ avec \enspace \Biggl \{ \begin{align*} (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \\ d = -ax_0 - by_0 -c z_0 \end{align*} $$
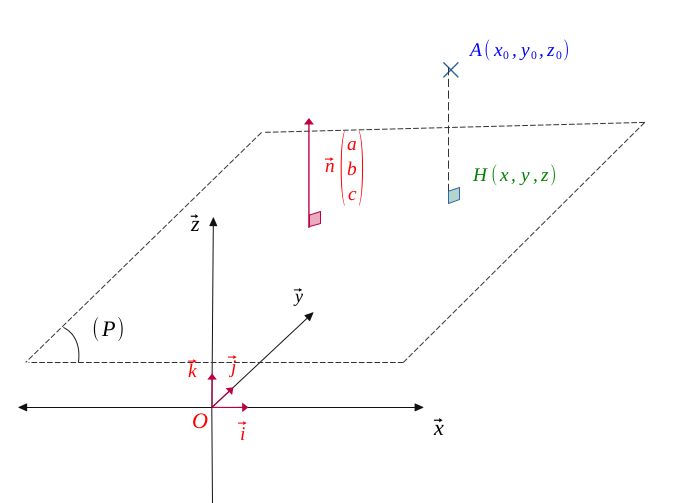
Soit un plan \(\mathcal{P}\) orthogonal au vecteur \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\) (avec \(a, b, c \) non nuls tous les trois), ayant pour équation :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, \ ax + by + cz + d = 0$$
La distance d'un point \(A(x_0, y_0, z_0)\) par rapport à ce plan \((\mathcal{P})\) se projettant orthogonalement sur ce même plan en \(H(x, y, z)\) vaut :
$$ d(A, \mathcal{P}) = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \\ d = -ax - by -c z \end{align*} $$
Projection d'une somme de vecteurs sur un plan
La projection d'une somme de vecteurs est la somme des projections de chaque vecteur
$$ \forall n \in \mathbb{N}, \ \forall (\vec{u_1}, \vec{u_2}, \ ..., \vec{u_n}), $$
$$ proj\left(\sum_{k=0}^n \overrightarrow{ u_k} \right) = \sum_{k=0}^n proj(\overrightarrow{u_k})$$
La sphère \((\mathcal{S})\) de rayon \(R\) et centrée en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$
$$ (avec \enspace (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3) $$
Le cylindre \((\mathcal{C})\) de rayon \(r\) et centré en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y) \in \hspace{0.05em}\mathbb{R}^2, $$
$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} r^2 = (x-x_0)^2 + (y-y_0)^2 $$
$$ (avec \enspace (x_0, y_0) \in \hspace{0.05em} \mathbb{R}^2) $$
Le cône \((\mathcal{C})\) de demi-angle \( \theta\), et centré en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} (x- x_0)^2 + (y- y_0)^2 = k(z-z_0)^2 $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ k = tan^2(\theta) \end{align*} $$
Passer des coordonnées cartésiennes en coordonnées sphériques
$$ \Biggl \{ \begin{align*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \\ z = R \ sin(\varphi) \end{align*} \qquad (\theta : longitude- \varphi : latitude) $$
$$avec \enspace \left \{ \begin{align*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{align*} \right \}$$

$$ \Biggl \{ \begin{align*} x = R \ sin(\psi) \ cos(\theta) \\ y = R \ sin(\psi) \ sin(\theta) \\ z = R \ cos(\psi) \end{align*} \qquad (\theta : longitude- \psi : colatitude) $$
$$avec \enspace \left \{ \begin{align*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \psi = arccos \left( \frac{z}{R} \right) \end{align*} \right \}$$
Soit une droite \((\mathcal{D})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et dirigée par un vecteur \(\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix}\) (avec \(a, b, c \) non nuls tous les trois) .

Comme \(M \in \mathcal{D}\), alors les vecteurs \(\vec{u}\) et \(\overrightarrow{AM}\) sont colinéaires. Soit :
$$ M(x, y, z) \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \overrightarrow{AM} = t \times \overrightarrow{u}$$
$$ \Longleftrightarrow \exists^{\infty} t \in \mathbb{R}, \enspace \begin{pmatrix} x -x_0 \\ y - y_0 \\z - z_0 \end{pmatrix} = \hspace{0.1em} \begin{pmatrix} ta \\ tb \\tc \end{pmatrix} $$
$$ \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x -x_0 = at\\ y - y_0 = bt \\z - z_0 = ct \end{Bmatrix} $$
L'équation paramétrique d'une droite \((\mathcal{D})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et dirigée par un vecteur \(\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix}\) est :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M(x, y, z) \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x = at + x_0 \\ y = bt + y_0 \\z = ct + z_0 \end{Bmatrix} $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \end{align*} $$
Le paramètre \(t\) est un paramètre libre qui peut prendre n'importe quelle valeur.
En effet, la droite \((\mathcal{D})\) s'étendant à l'infini, on obtient une formation de cette dernière en faisant varier \(t\), aboutissant à l'intersection de trois plans correspondant respectivement aux trois équations ; ce qui forme une suite de points dans l'espace.
Soit un plan \((\mathcal{P})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et orthogonal à un vecteur \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\)(avec \(a, b, c \) non nuls tous les trois). On dit que \(\vec{n}\) est un vecteur normal au plan.

Alors, tout point \(M(x, y, z)\) appartenant à ce plan est orthogonal à \(\vec{n}\).
$$ M(x, y, z) \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \overrightarrow{MA} \perp \vec{n}$$
Deux vecteur orthogonaux ont leur produit scalaire nul.
$$ \Longleftrightarrow \hspace{0.1em} \overrightarrow{MA} .\vec{n} = 0$$
$$ \Longleftrightarrow \begin{pmatrix} x -x_0 \\ y - y_0 \\z - z_0 \end{pmatrix} . \hspace{0.1em} \begin{pmatrix} a \\ b \\c \end{pmatrix} = 0$$
$$ a(x-x_0) + b(y-y_0) + c(z-z_0) = 0 $$
$$ ax - ax_0 + by - by_0 + cz -c z_0 = 0 $$
$$ ax + by + cz \hspace{0.1em} \underbrace{-ax_0 - by_0 -c z_0} _\text{\( (d \hspace{0.1em} \in \hspace{0.05em} \mathbb{R})\)} \hspace{0.1em} = 0 $$
$$ ax + by + cz + d = 0 $$
L'équation d'un plan \((\mathcal{P})\) dans l'espace, passant par un point \(A(x_0, y_0, z_0)\) et orthogonal à un vecteur \(\vec{u}\begin{pmatrix} a\\ b \\c \end{pmatrix}\) est :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M(x, y, z) \in \mathcal{P}(A, \vec{n}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} ax + by + cz + d = 0$$
$$ avec \enspace \Biggl \{ \begin{align*} (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \\ d = -ax_0 - by_0 -c z_0 \end{align*} $$
Soit un plan \((\mathcal{P})\) dans l'espace, orthogonal à un vecteur \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\)(avec \(a, b, c \) non nuls tous les trois).
Soit un point \(A(x_0, y_0, z_0)\) qui se projette orthogonalement sur ce plan \((\mathcal{P})\) en \(H(x, y, z)\).

On cherche à évaluer la distance \(AH\), distance la plus courte du point \(A\) au plan \((\mathcal{P})\).
Par la définition du produit scalaire, on a :
$$ \overrightarrow{AH} .\vec{n} = ||\overrightarrow{AH} || \times ||\overrightarrow{n} || \times cos(\overrightarrow{AH}, \overrightarrow{n}) $$
$$ \overrightarrow{AH} .\vec{n} = AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) \qquad (1)$$
D'autre part, avec le calcul du produit scalaire par le produit des coordonnées, on a :
$$ \overrightarrow{AH} .\vec{n} = a(x-x_0) + b(y-y_0) + c(z-z_0) $$
$$ \overrightarrow{AH} .\vec{n} = \hspace{0.1em} \underbrace{ax + by + c z} _\text{\( -d \)} \ -ax_0 - by_0 -c z_0 $$
$$ \overrightarrow{AH} .\vec{n} = -ax_0 - by_0 -c z_0 -d \qquad (2) $$
Étant donné que \((1)\) et \((2)\) sont équivalents, étant le même produit scalaire, on a :
$$ AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) = -ax_0 - by_0 -c z_0 -d $$
Calculant une distance, on peut passer en valeur absolue :
$$ \Bigl | AH \times \sqrt{a^2 + b^2 + c^2} \times (\pm 1) \Bigr | = \Bigl | -ax_0 - by_0 -c z_0 -d \Bigr | $$
$$AH = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\Bigl |\sqrt{a^2 + b^2 + c^2} \times (\pm 1) \Bigr |} $$
$$AH = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$
La distance d'un point \(A(x_0, y_0, z_0)\) extérieur au plan \((\mathcal{P})\) se projettant orthogonalement sur ce même plan en \(H(x, y, z)\) vaut :
$$ d(A, \mathcal{P}) = \frac{\Bigl | -ax_0 - by_0 -c z_0 -d \Bigr |}{\sqrt{a^2 + b^2 + c^2}} $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ (a, b, c) \in \hspace{0.05em} \mathbb{R}^3 \ trois \ nombres \ r \textit{é}els \ non \ nuls \ simultan\textit{é}ment \\ d = -ax - by -c z \end{align*} $$
Dans cette partie, le terme de projection signifira toujours projection orthogonale.
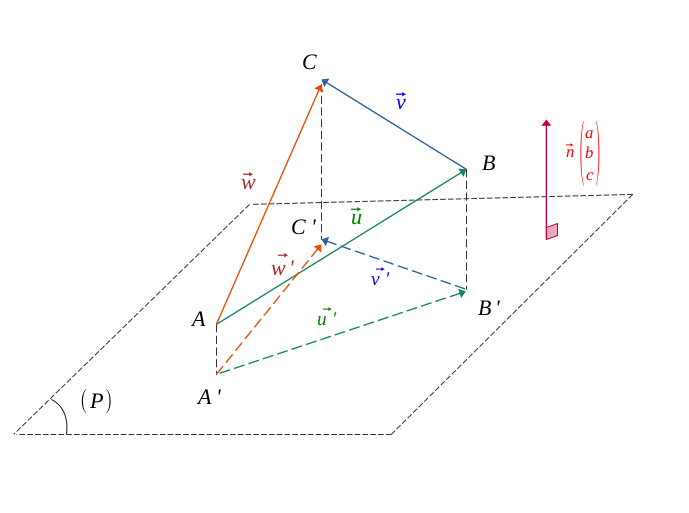
Soit un plan \((\mathcal{P})\) de vecteur normal \(\vec{n}\begin{pmatrix} a\\ b \\c \end{pmatrix}\), et deux vecteurs non nuls et non colinéaires à ce plan, \(\vec{u}\begin{pmatrix} x_1\\ y_1 \\z_1 \end{pmatrix}\) et \(\vec{v}\begin{pmatrix} x_2\\ y_2 \\z_2\end{pmatrix}\).
On appelle les deux vecteurs \(\vec{u'}\) et \(\vec{v'}\) les projections respectives des vecteurs \(\vec{u}\) et \(\vec{v}\) sur ce plan.
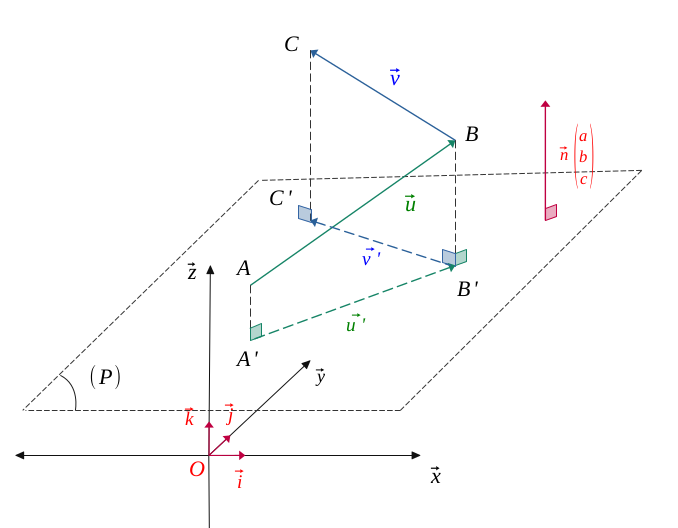
Par simplicité, on a placé les points \(A, B, C\) et leur projeté respectif \(A', B', C'\).
De même, soit \(\vec{w} = \vec{u} + \vec{v}\), la somme des vecteurs \(\vec{u}\) et \(\vec{v}\), et \(\vec{w'}\) le projeté de \( \vec{w}\) sur le plan.
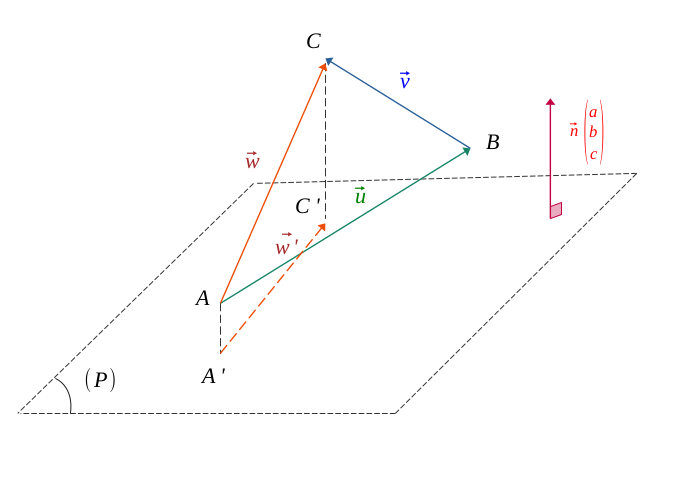
Dans le cas des points initiaux \(A, B, C\) et celui de leur projeté respectif \(A', B', C'\), on a la relation de Chasles qui s'applique :

$$ \Biggl \{ \begin{align*} \vec{u} + \vec{v} = \vec{w} \\ \vec{u}' + \vec{v}' = \ \vec{w}' \end{align*} $$
Par conséquent,
La projection d'une somme de vecteurs est la somme des projections de chaque vecteur
$$ \forall n \in \mathbb{N}, \ \forall (\vec{u_1}, \vec{u_2}, \ ..., \vec{u_n}), $$
$$ proj\left(\sum_{k=0}^n \overrightarrow{ u_k} \right) = \sum_{k=0}^n proj(\overrightarrow{u_k})$$
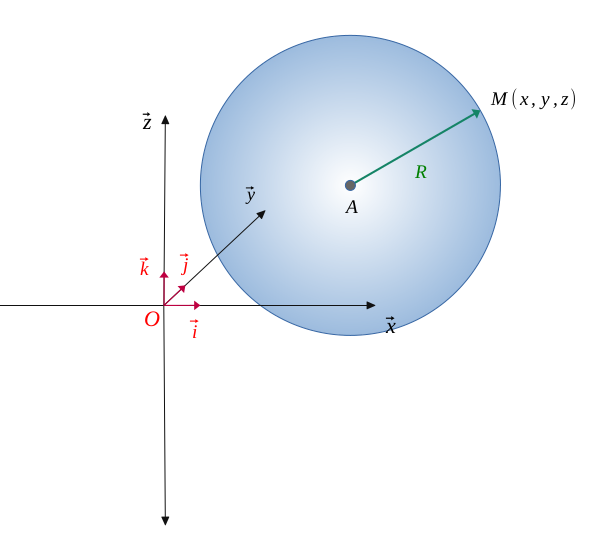
Soit une sphère \((\mathcal{S})\) de rayon \(R\) et centrée en \(A(x_0, y_0, z_0)\).

Sur cette sphère, tout point tout point \(M(x, y, z)\) se situe à égale distance du point \(A\), cette longueur étant celle du rayon \(R\).
On sait grâce au théorème de Pythagore, que la distance \( AB\) dans un espace tri-dimensionnel vaut:
$$\forall (A, B) \in \hspace{0.05em} (O, \vec{x}, \vec{y}, \vec{z})^2, $$
$$AB =\sqrt{(x_b - x_a)^2 + (y_b - y_a)^2 + (z_b - z_a)^2 }$$
Soit,
$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} AM = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 }$$
$$ R = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 }$$
$$ R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$
La sphère \((\mathcal{S})\) de rayon \(R\) et centrée en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M \in \mathcal{S}(A, R) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} R^2 = (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 $$
$$ (avec \enspace (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3) $$
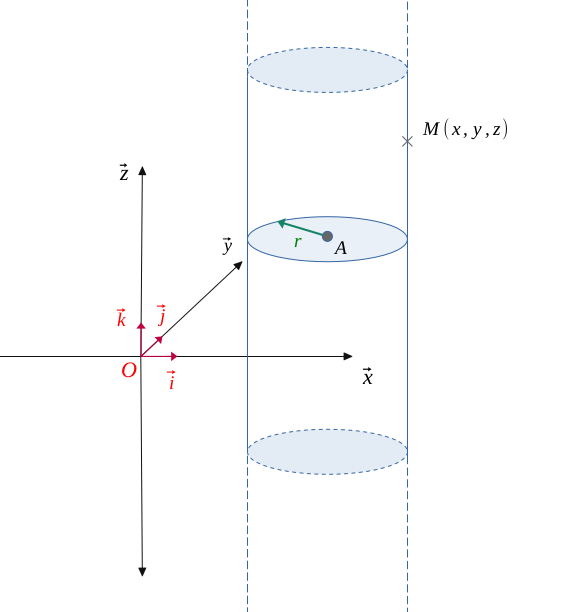
Soit un cylindre vertical \((\mathcal{C})\) de rayon \(r\) et centré en \(A(x_0, y_0, z_0)\).

Dans le plan \((O, \overrightarrow{i}, \overrightarrow{j})\), le cylindre décrit un cercle.
On sait grâce au théorème de Pythagore, que la distance \( AB\) dans le plan vaut:
$$\forall (A, B) \in \hspace{0.05em} (O, \vec{x}, \vec{y})^2, $$
$$AB = \sqrt{ (x_b - x_a)^2 + (y_b - y_a)^2} $$
On a alors,
$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} AM = \sqrt{(x-x_0)^2 + (y-y_0)^2 }$$
$$ r = \sqrt{(x-x_0)^2 + (y-y_0)^2 }$$
$$ r^2 = (x-x_0)^2 + (y-y_0)^2 $$
L'axe vertical \(z\) peut lui prendre n'importe quelle valeur, c'est donc une variable libre.
Le cylindre \((\mathcal{C})\) de rayon \(r\) et centré en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y) \in \hspace{0.05em}\mathbb{R}^2, $$
$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} r^2 = (x-x_0)^2 + (y-y_0)^2 $$
$$ (avec \enspace (x_0, y_0) \in \hspace{0.05em} \mathbb{R}^2) $$
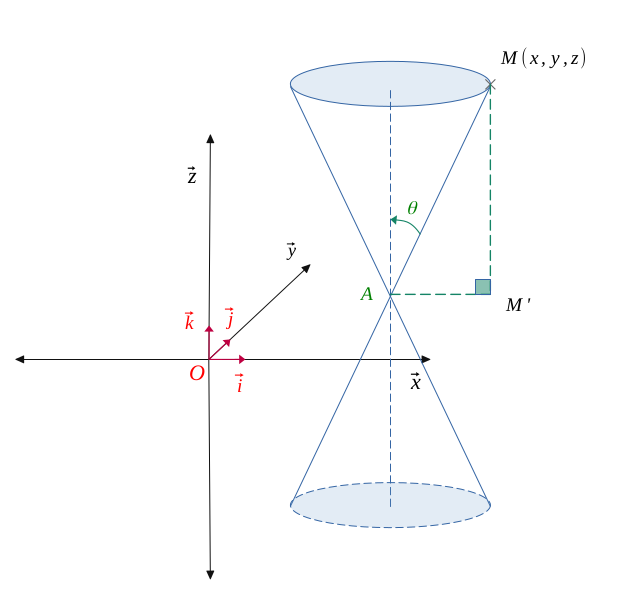
Soit un cône vertical \((\mathcal{C})\) de demi-angle \( \theta\), et centré en \(A(x_0, y_0, z_0)\).

Sur la figure ci-dessous, on peut voir que :
$$ M \in \mathcal{C}(A, \theta) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} tan(\theta) = \frac{AM'}{AM} $$
$$ \Longleftrightarrow \hspace{0.1em} tan(\theta) = \frac{\sqrt{ (x- x_0)^2 + (y- y_0)^2} }{|z-z_0|} $$
$$ tan^2(\theta) = \ \frac{ (x- x_0)^2 + (y- y_0)^2 }{(z-z_0)^2} $$
$$ (x- x_0)^2 + (y- y_0)^2 = (z-z_0)^2 tan^2(\theta) $$
Le cône \((\mathcal{C})\) de demi-angle \( \theta\), et centré en \(A(x_0, y_0, z_0)\) a pour équation dans l'espace :
$$ \forall (x, y, z) \in \hspace{0.05em}\mathbb{R}^3, $$
$$ M \in \mathcal{C}(A, r) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} (x- x_0)^2 + (y- y_0)^2 = k(z-z_0)^2 $$
$$ avec \enspace \Biggl \{ \begin{align*} (x_0, y_0, z_0) \in \hspace{0.05em} \mathbb{R}^3 \\ k = tan^2(\theta) \end{align*} $$
Dans certains cas, il peut être utile de passer en coordonnées sphériques (en deux dimensions : coordonnées polaires), notamment lorsque l'on travaille avec des sphères.
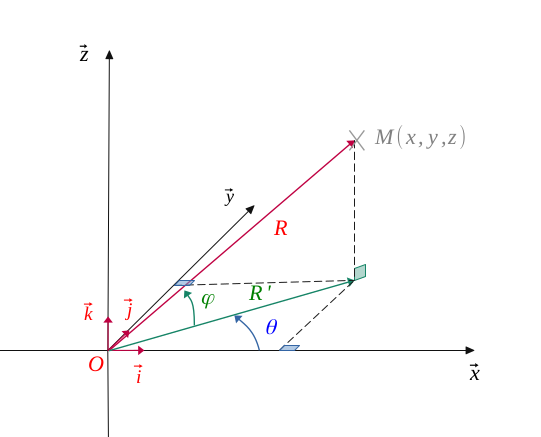
Dans un repère orthonormé habituel dans l'espace \((O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\), on a représenté un point \(M(x, y, z)\).

Soit \(R\) représentant la distance de ce point à l'origine et \(R'\) sa projection sur le plan horizontal \((O, \overrightarrow{i}, \overrightarrow{j})\).
De même, on a appelé \(\theta\) l'angle formé par l'axe des abscisses \((O, \overrightarrow{i})\) et \(R'\), et \(\varphi\) l'angle formé par \(R'\) et \(R\).
$$ \Biggl \{ \begin{align*} \theta = (\overrightarrow{Ox}, \overrightarrow{R'}) \\ \varphi= (\overrightarrow{R'}, \overrightarrow{R})\end{align*} $$
Sur la figure qui suit, on a représenté le point \(M'\), projeté sur point \(M\) sur le plan horizontal \((O, \overrightarrow{i}, \overrightarrow{j})\).
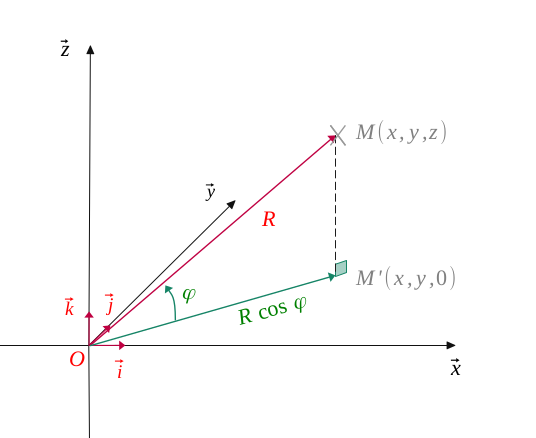
Avec les règles de trigonométrie classiques, on voit aisément que :
$$ \Biggl \{ \begin{align*} z = R \ sin(\varphi) \\ R' = R \ cos(\varphi) \end{align*} $$
Maintenant, en travaillant avec une vue de face du plan horizontal \((O, \overrightarrow{i}, \overrightarrow{j})\), on peut calculer les coordonnées correspondantes à \(x\) et \(y\).
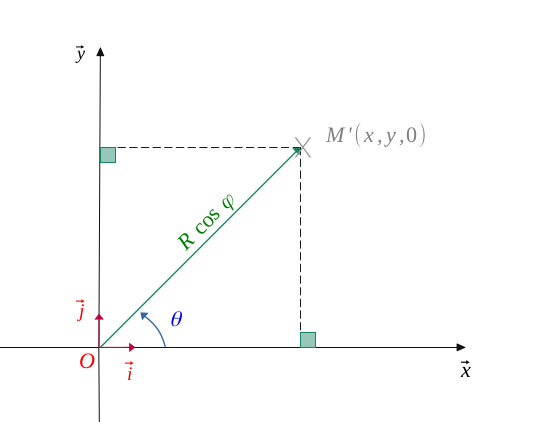
On a :
$$ \Biggl \{ \begin{align*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \end{align*} $$
Enfin, la distance \(R\) est facilement calculable à partir des coordonnées cartésiennes \((x, y, z)\) :
$$R =\sqrt{x^2 +y^2 +z^2 }$$
De même, on peut obtenir les angles \(\theta\) et \(\varphi\) par :
$$ \Biggl \{ \begin{align*} \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{align*} $$
Alors,
$$ \Biggl \{ \begin{align*} x = R \ cos(\varphi) \ cos(\theta) \\ y = R \ cos(\varphi) \ sin(\theta) \\ z = R \ sin(\varphi) \end{align*} \qquad (\theta : longitude- \varphi : latitude) $$
$$avec \enspace \left \{ \begin{align*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \varphi = arcsin \left( \frac{z}{R} \right) \end{align*} \right \}$$
Il existe une autre manière de représenter les coordonnées sphériques; on peut utiliser la colatitude à la place de la latitude.
On a alors un nouvel angle \(\psi\) qui démarre de l'axe vertical \(\overrightarrow{Oz}\) vers \(R\) dans le sens antitrigonométrique.

$$ \Biggl \{ \begin{align*} \theta = (\overrightarrow{Ox}, \overrightarrow{R'}) \\ \varphi= (\overrightarrow{Oz}, \overrightarrow{R})\end{align*} $$
Ce qui donne, en appliquant le même raisonnement :
$$ \Biggl \{ \begin{align*} x = R \ sin(\psi) \ cos(\theta) \\ y = R \ sin(\psi) \ sin(\theta) \\ z = R \ cos(\psi) \end{align*} \qquad (\theta : longitude- \psi : colatitude) $$
$$avec \enspace \left \{ \begin{align*} R =\sqrt{x^2 +y^2 +z^2 } \\ \theta = arctan \left( \frac{y}{x} \right) \\ \psi = arccos \left( \frac{z}{R} \right) \end{align*} \right \}$$
Cherchons l'intersection \((\mathcal{P} \cap \mathcal{P}') \) entre les deux plans \((\mathcal{P}) \) et \((\mathcal{P}') \).
$$ (\mathcal{S}) \ \Biggl \{ \begin{align*} \ \ 3x \ - \ y \ + z \hspace{1.8em}= 0 \qquad (\mathcal{P}) \\ -2x +2y + z + 1 = 0 \qquad (\mathcal{P}') \end{align*} $$
On échelonne le système \((\mathcal{S})\) en faisant la combinaison linéaire \( 2(\mathcal{P}) \) + \( 3(\mathcal{P}') \).
$$ (\mathcal{S}) \ \Biggl \{ \begin{align*} 3x - y \ + z = 0 \hspace{5em} (\mathcal{P}) \\ \ \ \ \ 4y +5 z = -3 \qquad \qquad (2(\mathcal{P}) + 3(\mathcal{P}') ) \end{align*} $$
Le système est de rang \(2\), alors l'intersection est une droite qu'on notera \( (\mathcal{D})\). De plus, le paramètre \( z \) est une variable libre et :
$$z = \frac{4y-3}{5} \Longleftrightarrow y = \frac{-5z-3}{4} $$
Alors, on résout le système par remontée et on trouve :
$$ \left \{ \begin{align*} x = \frac{-3z-1}{4} \\ y = \frac{-5z-3}{4} \\ z= z \end{align*} \right \} $$
On choisit comme valeur \( z = 0 \) pour fixer un point de la droite \( (\mathcal{D})\). Alors \( A\left(-\frac{1}{4},-\frac{3}{4}, 0 \right) \in \mathcal{D}\).
Par ailleurs, on voit que le vecteur \(\vec{u}\begin{pmatrix} -\frac{3}{4} \\ - \frac{5}{4} \\ \hspace{1em} 1 \end{pmatrix}\) dirige la droite \( (\mathcal{D})\), alors celle-ci a pour équation :
$$ M(x, y, z) \in \mathcal{D}(A, \vec{u}) \hspace{0.1em} \Longleftrightarrow \hspace{0.1em} \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x + \frac{1}{4} = -\frac{3}{4}t\\ y + \frac{3}{4} = -\frac{5}{4}t \\z = t \end{Bmatrix} $$
Soit,
$$(\mathcal{P} \cap \mathcal{P}')=(\mathcal{D}) \Longleftrightarrow \exists^{\infty} t \in \mathbb{R}, \enspace \begin{Bmatrix} x = -\frac{3}{4}t - \frac{1}{4}\\ y = -\frac{5}{4}t -\frac{3}{4} \\z = t \end{Bmatrix} $$
Cherchons l'intersection \((\mathcal{D} \cap \mathcal{P}) \) entre une droite \((\mathcal{D}) \) et un plan \((\mathcal{P}) \).
$$ (\mathcal{D}) \ \Biggl \{ \begin{align*} x = t-1 \\ y = -2t + 3 \\ z= -t+5 \end{align*} $$
$$ 2x + y -3z + 6 = 0 \qquad (\mathcal{P})$$
On injecte les coordonnées de \((\mathcal{D}) \) dans celles de \((\mathcal{P}) \), et on résout \((L) \) :
$$ 2(t-1) -2t + 3 -3(-t+5) + 6 = 0 \qquad (L)$$
$$ 2t-2-2t+3+3t -15 +6 = 0 \qquad (L)$$
$$ 3t-8 = 0 \Longleftrightarrow t = \frac{8}{3} \qquad (L)$$
Comme \(t \) est unique, il y a un point d'intersection, qu'on notera \(A\).
On détermine alors ce point grâce à l'équation paramétrique de la droite \((\mathcal{D}) \).
Ce point d'intersection est donc :
$$ (\mathcal{D} \cap \mathcal{P}) = A\left(\frac{5}{3}; -\frac{7}{3}; \frac{7}{3} \right)$$
Cherchons l'intersection \((\mathcal{D} \cap \mathcal{D}') \) entre deux droites \((\mathcal{D}) \) et \((\mathcal{D}') \).
$$ (\mathcal{D}) \ \Biggl \{ \begin{align*} x = 2t-1 \\ y = -t-2 \\ z= t+2 \end{align*} $$
$$ (\mathcal{D}') \ \Biggl \{ \begin{align*} x = s+1 \\ y = 3s-1\\ z= 2s+1\end{align*} $$
On a le système suivant :
$$ (\mathcal{D} \cap \mathcal{D}') \ \Longleftrightarrow \Biggl \{ \begin{align*} 2t-1 = s+1 \\ -t-2 = 3s-1\\ t +2 = 2s+1\end{align*} $$
$$ (\mathcal{D} \cap \mathcal{D}') \ \Longleftrightarrow \ \Biggl \{ \begin{align*} 2t-s = 5 \ \ \qquad (L_1) \\ -t-3s = 1 \qquad (L_2) \\ t-2s = -1 \qquad (L_3) \end{align*} $$
On résout d'abord les deux premières équations. On effectue \( (L_1 + 2 L_2)\) :
$$-7s = 7 \qquad (L_1 + 2 L_2) \ \Longrightarrow \ s = -1 \ \Longrightarrow \ t = 2 $$
Cette solution ne convient pas à la troisième \( (L_3)\) car :
$$2 - 2\times(-1) = 4\neq -1 $$
Alors, comme il n'existe aucun couple \( (t, s) \in \hspace{0.05em} \mathbb{R}^2\) qui conviennent aux deux équations paramétriques des deux droites \((\mathcal{D}) \) et \((\mathcal{D}') \), elles n'ont pas de point d'intersection.
$$(\mathcal{D} \cap \mathcal{D}') = \emptyset $$
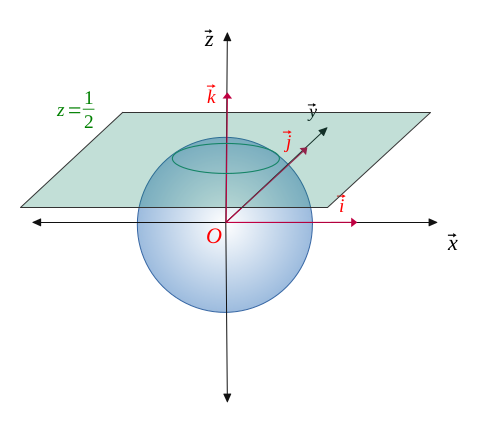
Cherchons l'intersection \((\mathcal{P} \cap \mathcal{S}) \) entre un plan \((\mathcal{P}) \) et une sphère \((\mathcal{S}) \).
$$ z = \frac{1}{2} \qquad (\mathcal{P}) $$
$$ x^2 + y^2 + z^2 = 1 \qquad (\mathcal{S}) $$
On injecte \((\mathcal{P}) \) dans \((\mathcal{S}) \) :
$$ x^2 + y^2 = \frac{3}{4} $$
Alors, on obtient une équation pour les coordonnées \((x,y) \in \hspace{0.05em} \mathbb{R}^2 \). C'est en revanche l'équation d'un cône de rayon \(R = \frac{\sqrt{3}}{2}\), il faut alors conserver l'équation du plan \((\mathcal{P}) \) pour fixer le cône et par conséquent obtenir un cercle.
Alors, l'intersection entre \((\mathcal{P}) \) et \((\mathcal{S}) \) est modélisée par la double équation :
$$ (\mathcal{P} \cap \mathcal{S}) \ \Longleftrightarrow \ \Biggl \{ \begin{align*} x^2 + y^2 = \frac{3}{4} \\ z = \frac{1}{2} \end{align*} $$
 Retour en haut de page
Retour en haut de page