







Dans le cas général, lorsqu'une corde d'un cercle intercepte deux côtés d'un triangle inscrit, l'angle opposé formé est égal à la moitié de l'arc formé par la corde.
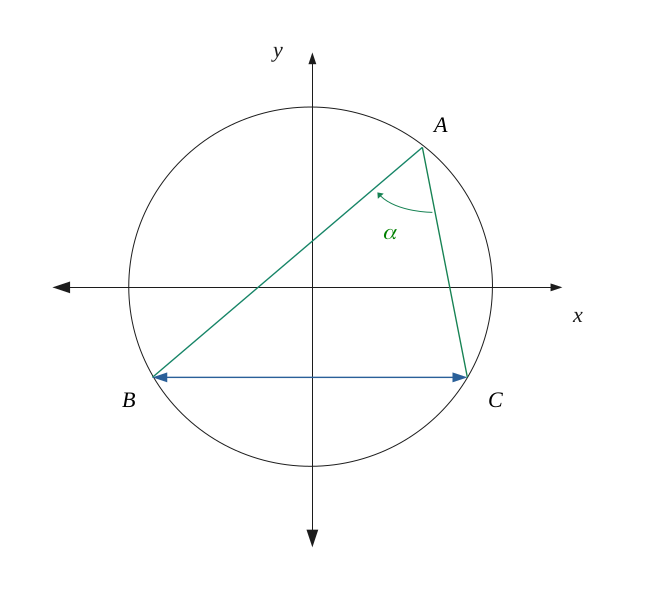
$$ \alpha = \frac{\overset{\frown}{BC}}{2} $$
Comme dans le cas où la corde est la diamètre du cercle, l'arc \( \overset{\frown}{BC} \enspace = \pi \), tel que la figure suivante :
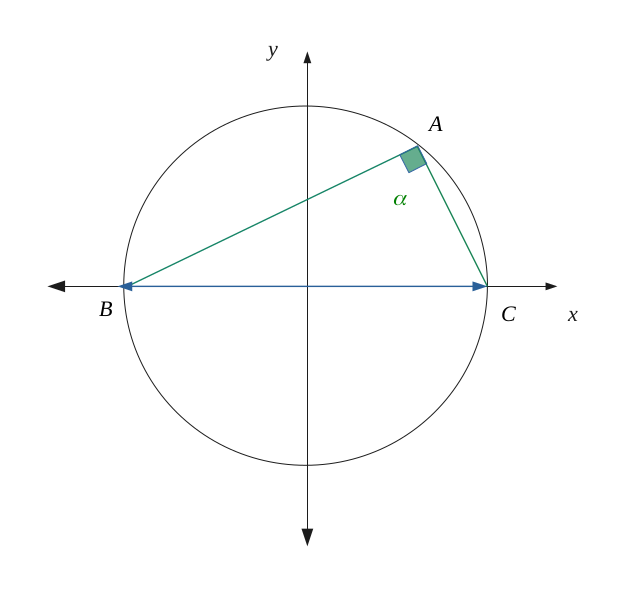
Alors \( \alpha = \frac{\pi}{2}\), et le triangle sera rectangle.
Dans un cercle, si un triangle inscrit a pour plus grand côté le diamètre de ce cercle, alors ce triangle est rectangle.
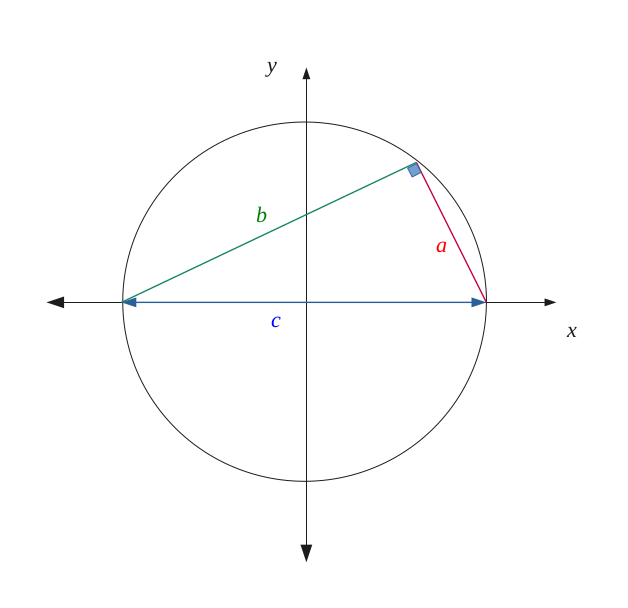
Pour cela, on se munit d'un repère orthonomé \( (0, \vec{x}, \vec{y}) \).
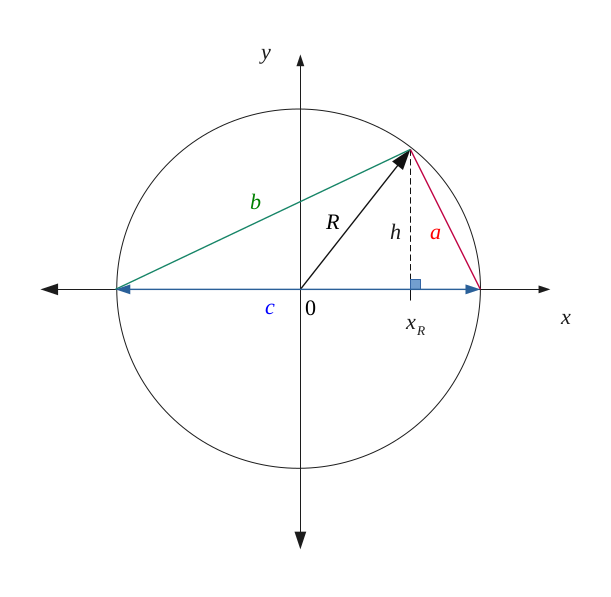
On a appelé les côtés du triangle \( a, b, c \), et on y a projeté une hauteur \( h \) sur la longueur \( c \), avec comme point d'intersection \( x_R \) .
De même, on a tracé le rayon \( R \) du cercle pointant vers le sommet entre \( a \) et \( b \) du triangle.
On va chercher à démontrer que le triangle \( \{a, b, c \} \) est rectangle entre \( a \) et \( b \).
On sait par la réciproque du théorème de Pythagore que :
$$ a^2 + b^2 = c^2 \Longrightarrow a \perp b \qquad \bigl(Pythagore \enspace(réciproque) \bigr) $$
C'est ce que nous allons démontrer.
On applique le théorème de Pythagore sur les trois rectangles :
- celui formé par \( \{h, (R - x_r), a \} \)
- celui formé par \( \{h, (R + x_r), b\} \)
- celui formé par \( \{h, x_R, R \} \)
On alors les égalités suivantes :
$$ h^2 + (R - x_R)^2 = a^2 \qquad (1) $$
$$ h^2 + (R + x_R)^2 = b^2 \qquad (2) $$
$$ h^2 + x_R^2 = R^2 \Longleftrightarrow h^2 = R^2 - x_R^2\qquad (3) $$
Injectons l'expression de \( h^2 \) de l'expression \( (3) \) dans \( (1) \) et \( (2) \), on obtient alors un nouveau couple d'égalité :
$$ \Biggl \{ \begin{gather*} R^2 - x_R^2 + (R - x_R)^2 = a^2 \qquad (4) \\ R^2 - x_R^2 + (R + x_R)^2 = b^2 \qquad (5) \end{gather*} $$
Calculons maintenant \( a^2 + b^2 \) en effectuant l'opération \( (4) + (5) \) :
$$ a^2 + b^2 = R^2 - x_R^2 + (R - x_R)^2 + R^2 - x_R^2 + (R + x_R)^2 $$
$$ a^2 + b^2 = R^2 - x_R^2 + R^2 - 2R.x_R + x_R^2 + R^2 - x_R^2 + R^2 + 2R.x_R + x_R^2 $$
De nombreux termes s'annulent, et on obtient :
$$ a^2 + b^2 = 4R^2 $$
$$ a^2 + b^2 = (2R)^2 $$
Par ailleurs, on sait que :
$$ c = 2R $$
Car c'est notre diamètre par hypothèse.
Soit finalement :
$$ a^2 + b^2 = c^2 $$
Avec la la réciproque du théorème de Pythagore, on a montré que le triangle \( \{a, b, c \} \) est rectangle entre \( a \) et \( b \).
Alors,
Dans un cercle, si un triangle inscrit a pour plus grand côté le diamètre de ce cercle, alors ce triangle est rectangle.
 Retour en haut de page
Retour en haut de page