








Nous allons calculer une formule du nombre \(\pi \) en passant par une méthode géométrique.
Pour cela, nous alons passer par plusieurs iérations successives.
Le nombre \(\pi \) correspond au rapport entre le demi-périmètre d'un cercle de rayon \( R = 1\).
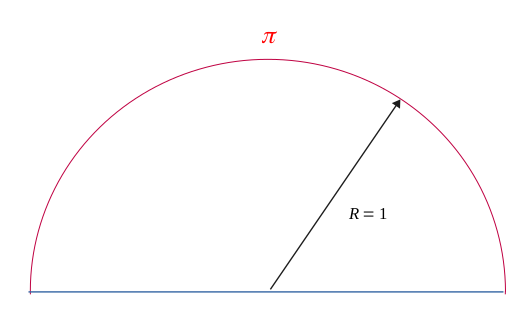
$$ \pi = \frac{P_{(R=1)}}{2}$$
La formule théorique que nous allons démontrer est :
$$ \pi = lim_{n \to +\infty} \enspace 2^{n + 1} \sqrt{2 - \underbrace{ \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2...}}} }} _\text{n} } $$ (avec \( n\) le nombre de \( 2\) présents à la suite sous la seconde racine)
Comme nous l'avons dit, nous allons effectuer plusieurs itérations successives pour retrouver cette formule.
Nous avons représenté un cercle de rayon \( R = 1 \), ainsi que son carré interne.
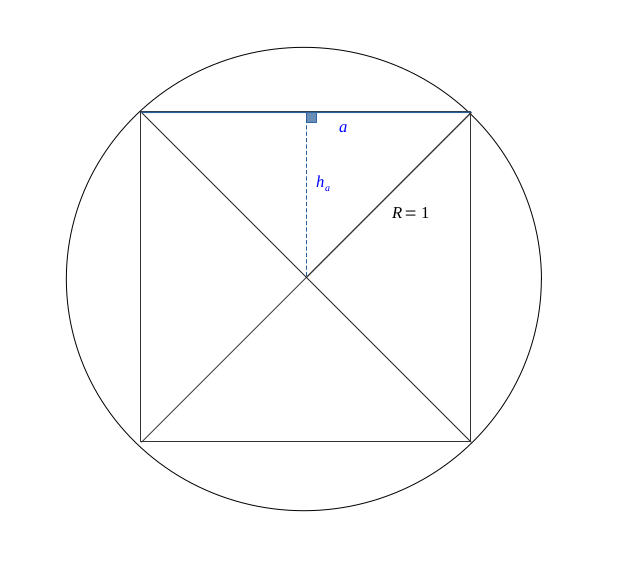
Nous allons partir du principe que :
$$ \pi \approx 2a $$
ce qui est une première approximation grossière.
Calculons la valeur de \( a \).
Avec le théorème de Pythagore, on a :
$$ a^2 = 1^2 + 1^2 $$
$$ a = \sqrt{2} $$
Ce que nous donne une valeur de \(\pi \) d'environ :
$$ \pi \approx 2a $$
$$ \pi \approx 2\sqrt{2} $$
$$ \pi \approx 2,82 $$
Pour cette deuxième approximation, nous allons choisir une longueur qui se rapproche plus du cercle, et nous l'avons representé en rouge.
C'est la base du triangle isocèle ayant comme une des longueurs égales, la demi-diagonale du carré interne.
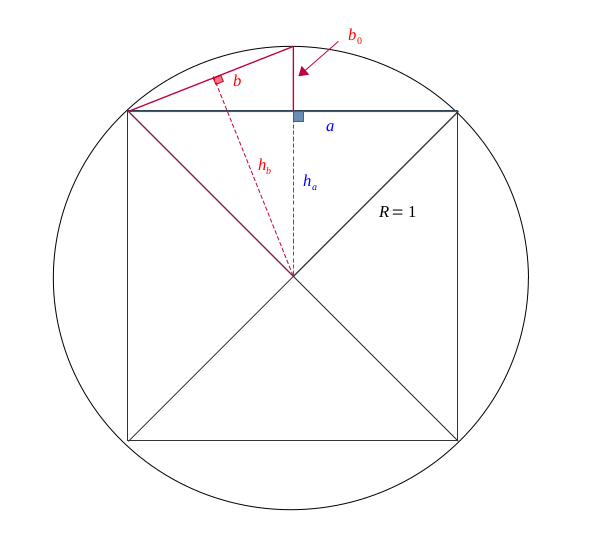
Pour approximer la valeur de \(\pi \) en suivant le demi-périmètre, nous aurons besoin cette fois-ci de quatre fois cette longueur. Soit :
$$ \pi \approx 4b $$
Toujours par le théorème de Pythagore, on calcule \( b \) :
$$ b^2 = \left(\frac{a}{2}\right)^2 + b_0^2 $$
$$ b^2 = \frac{a^2}{4} + (1 - h_a)^2 $$
$$ b^2 = \frac{a^2}{4} + \left(1 - \frac{a}{2}\right)^2 $$
$$ b^2 = \frac{a^2}{2} + 1 - a $$
On avait trouvé pour \( a \) :
$$ a = \sqrt{2} $$
Soit :
$$ b = \sqrt{2 - \sqrt{2}} $$
Ce que nous donne :
$$ \pi \approx 4b $$
$$ \pi \approx 4\sqrt{2 - \sqrt{2}} $$
$$ \pi \approx 3,06 $$
On voit que l'on commence à s'approcher doucement de \( \pi = 3,14 \dots)
Nous continuons la même démarche avec une longueur qui se rapetisse toujours encore un peu pour coller au cercle.
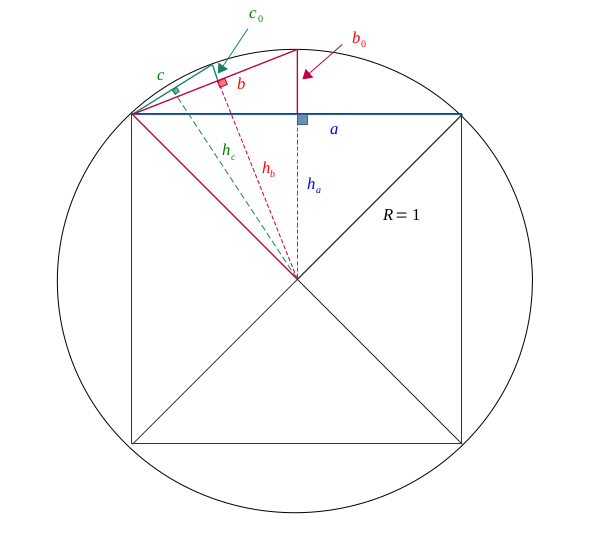
$$ \pi \approx 8c $$
On a :
$$ c^2 = \left(\frac{b}{2}\right)^2 + c_0^2 $$
$$ c^2 = \frac{b^2}{4} + (1 - h_b)^2 $$
Nous avons ici besoin de calculer \( h_b \) :
$$ R^2 = h_b^2 + \left(\frac{b}{2}\right)^2 $$
$$ h_b^2 = R^2 - \left(\frac{b}{2}\right)^2 $$
On avait calculé que \( b = 2 - \sqrt{2}\), soit :
$$ h_b^2 = 1^2 - \left(\frac{2 - \sqrt{2}}{4}\right) $$
$$ h_b^2 = 1 - \frac{1}{2} + \frac{\sqrt{2}}{4} $$
$$ h_b = \sqrt{\frac{1}{2} + \frac{\sqrt{2}}{4}} $$
$$ h_b = \frac{1}{2} \sqrt{2 + \sqrt{2}} $$
Remplaçons maintenant \( h_b \) par la valeur trouvée, nous avions :
$$ c^2 = \frac{b^2}{4} + (1 - h_b)^2 $$
Soit :
$$ c^2 = \frac{b^2}{4} + \left(1 - \frac{1}{2} \sqrt{2 + \sqrt{2}} \right)^2 $$
On avait trouvé pour \( b \) :
$$ b = \sqrt{2 - \sqrt{2}} $$
D'où,
$$ c^2 = \frac{2 - \sqrt{2}}{4} + 1 - 2 \times \frac{1}{2} (2 + \sqrt{2}) + \frac{2 + \sqrt{2}}{4} $$
$$ c = \sqrt{2 - \sqrt{2+ \sqrt{2 }} } $$
Ce que nous donne :
$$ \pi \approx 8c $$
$$ \pi \approx 8\sqrt{2 - \sqrt{2+ \sqrt{2 }} } $$
$$ \pi \approx 3,12 $$
Continuons maintenant en imaginant une nouvelle longueur \( d \), (trop petite pour être dessinée), trouvée par le même procédé que pour \( b \) et \( c \).
$$ \pi \approx 16d $$
On a :
$$ d^2 = \left(\frac{c}{2}\right)^2 + d_0^2 $$
$$ d^2 = \frac{c^2}{4} + (1 - h_c)^2 $$
Nous avons ici besoin de calculer \( h_c \) :
$$ R^2 = h_c^2 + \left(\frac{c}{2}\right)^2 $$
$$ h_c^2 = R^2 - \left(\frac{c}{2}\right)^2 $$
On avait \( c = \sqrt{2 - \sqrt{2+ \sqrt{2 }} } \), soit :
$$ h_c^2 = 1^2 - \left(\frac{2 - \sqrt{2+ \sqrt{2 }} }{4}\right) $$
$$ h_c = 1 - \frac{1}{2} + \frac{\sqrt{2+ \sqrt{2}}}{4} $$
$$ h_c = \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} $$
Remplaçons maintenant par la valeur trouvée, nous avions :
$$ d^2 = \frac{c^2}{4} + (1 - h_c)^2 $$
Soit :
$$ d^2 = \frac{c^2}{4} + \left(1 - \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} \right)^2 $$
On avait trouvé pour \( c \) :
$$ c = \sqrt{2 - \sqrt{2+ \sqrt{2 }} } $$
D'où,
$$ d^2 = \frac{ \sqrt{2 - \sqrt{2+ \sqrt{2 }} }}{4} + 1 - 2 \times \frac{1}{2} \sqrt{2 + \sqrt{2 + \sqrt{2}}} + \frac{2 + \sqrt{2 + \sqrt{2}}}{4} $$
$$ d = \sqrt { 2 - \sqrt { 2 + \sqrt { 2+ \sqrt{2}}} } $$
Ce que nous donne :
$$ \pi \approx 16d $$
$$ \pi \approx 16\sqrt { 2 - \sqrt { 2 + \sqrt { 2+ \sqrt{2}}} } $$
$$ \pi \approx 3,13 $$
En répétant cette procédure à l'infini, on finit par obtenir une généralisation.
Récapitulons.
Nous avons trouvé ces différentes valeurs pour \( \pi \) :
$$ \pi \approx 2\sqrt{2} \qquad (n = 0) $$
$$ \pi \approx 4\sqrt{2 - \sqrt{2}} \qquad (n = 1) $$
$$ \pi \approx 8\sqrt{2 - \sqrt{2+ \sqrt{2 }} } \qquad (n = 2) $$
$$ \pi \approx 16\sqrt { 2 - \sqrt { 2 + \sqrt { 2+ \sqrt{2}}} } \qquad (n = 3) $$
Nous voyons bien qu'il est alors possible de généraliser cette valeur, en faisant tendre \( n \to \infty \).
Et finalement :
$$ \pi = lim_{n \to +\infty} \enspace 2^{n + 1} \sqrt{2 - \underbrace{ \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2...}}} }} _\text{n} } $$ (avec \( n\) le nombre de \( 2\) présents à la suite sous la seconde racine)
 Retour en haut de page
Retour en haut de page