La puissance d'un point par rapport à un cercle

Cas 1 : Point intérieur au cercle

Si un point $ O$ est l'intersection entre deux cordes $ (AB )$ et $ (CD )$ d'un cercle à l'intérieur de celui-ci, et telles que la figure suivante :

Puissance d'un point par rapport à un cercle - point intérieur (avec les angles)

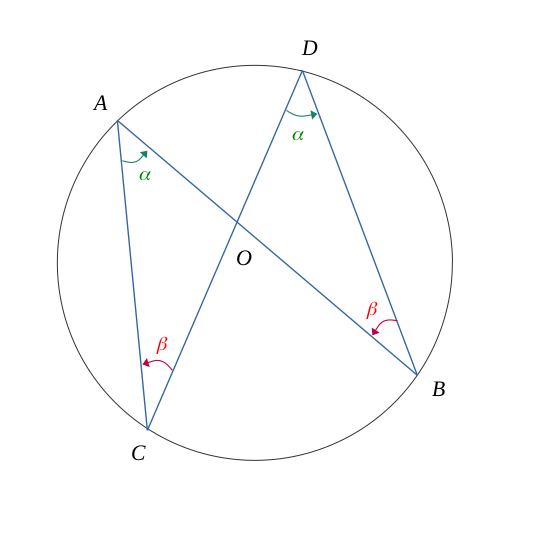
Alors, les deux triangles $ AOC $ et $ DOB $ sont semblables, et le produit entre les longueurs respectivement proportionnelles en partant du point $O$ vaut :

$$\overline{OA} \times \hspace{0.05em} \overline{OB} =\hspace{0.05em} \overline{OC} \times \overline{OD}$$

Cas 2 : Point extérieur au cercle

Si un point $ O$ est l'intersection entre deux cordes $ (AC )$ et $ (DB )$ d'un cercle à l'extérieur de celui-ci, et telles que la figure suivante :

Puissance d'un point par rapport à un cercle - point extérieur (avec les angles)

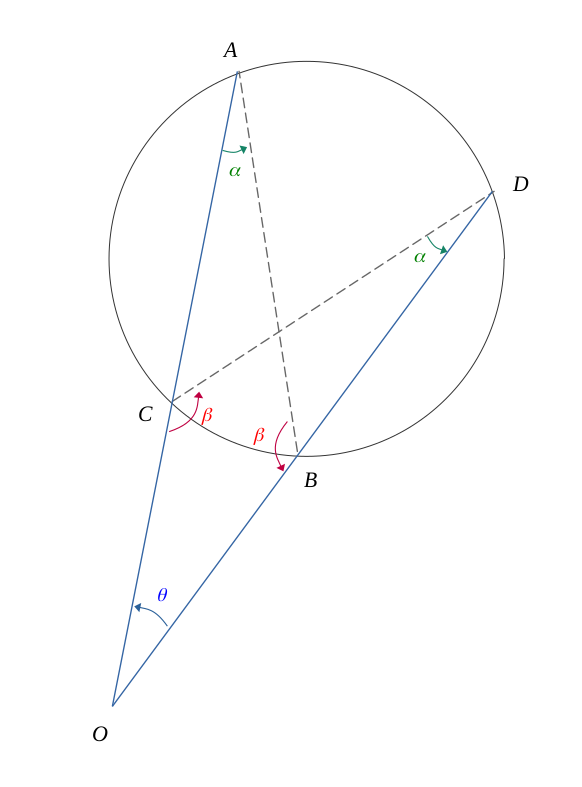
Alors, les deux triangles $ ABO $ et $ DCO $ sont semblables, et le produit entre les longueurs respectivement proportionnelles en partant du point $O$ vaut :

$$\overline{OA} \times \hspace{0.05em} \overline{OB} =\hspace{0.05em} \overline{OC} \times \overline{OD}$$

Cas 3 : Point extérieur au cercle avec une tangente

Si un point $ O$ est l'intersection entre une corde $ (AC )$ du cercle et une tangente à ce même cercle passant par $ T$, et telles que la figure suivante :

Puissance d'un point par rapport à un cercle - point extérieur et une tangente (avec les angles)

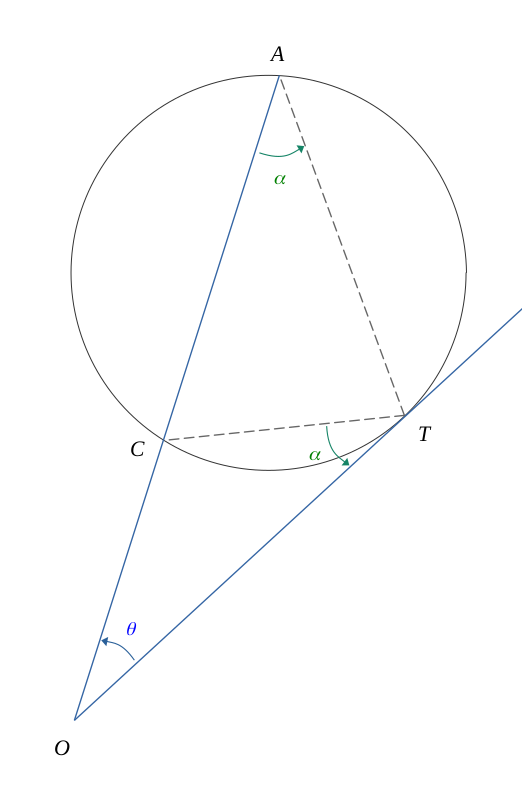
Alors, les deux triangles $ OAT $ et $ CTO $ sont semblables, et le produit entre les longueurs respectivement proportionnelles en partant du point $O$ vaut :

$$\overline{OA} \times \hspace{0.05em} \overline{OC} =\hspace{0.05em} \overline{OT} ^2$$

Cas 4 : Point extérieur au cercle avec deux tangentes

Si un point $ O$ est l'intersection entre deux tangentes au cercle passant respectivement par $ T$ et $ T'$, et telles que la figure suivante :

Puissance d'un point par rapport à un cercle - point extérieur et deux tangentes (avec les angles)

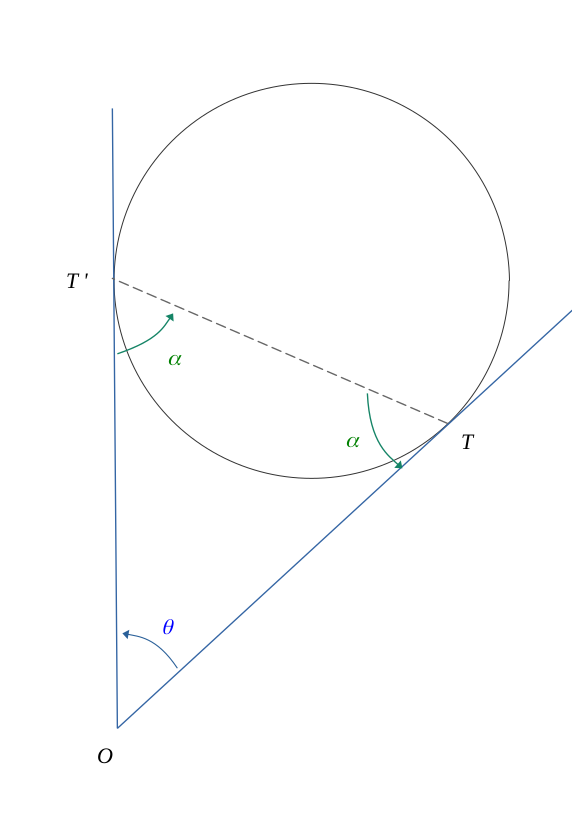
Alors, le triangle $ OTT' $ est un triangle isocèle, et dans ce cas :

$$\overline{OT} = \hspace{0.05em} \overline{OT'}$$

Démonstrations

Cas 1 : Point intérieur au cercle

Soit un cercle et deux cordes $AB$ et $CD$ telle que la figure suivante :

Puissance d'un point par rapport à un cercle - point intérieur

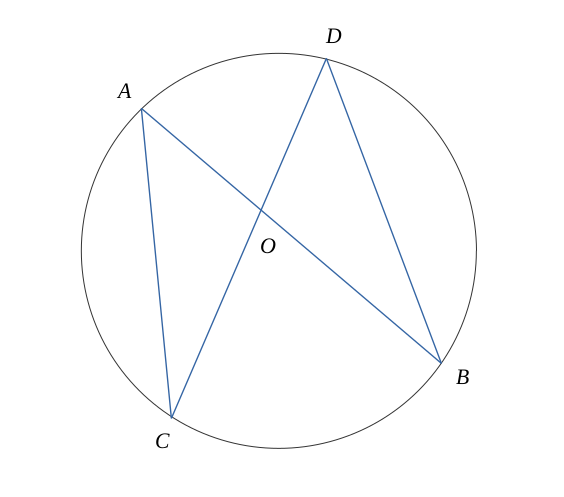
Le point $O$ est le point d'intersection entre les droites $(AB)$ et $(CD)$ à l'intérieur du cercle.

Les angles $ \widehat{BAC}$ et $ \widehat{BDC}$ inteceptent le même arc $ \overset{\frown}{BC}$ sur le cercle. Ils sont donc égaux.

$$ \widehat{BAC} = \widehat{BDC} = \alpha $$

De la même manière, les angles $ \widehat{ABD}$ et $ \widehat{ACD}$ inteceptent le même arc $ \overset{\frown}{AD}$ sur le cercle.

$$ \widehat{ABD} = \widehat{ACD} = \beta $$

Les deux triangles $ AOC $ et $ DOB $ ayant deux angles deux-à-deux respectivement égaux, ils sont semblables.

On alors les proportions suivantes :

$$ \frac{OA}{OC} = \frac{OD}{OB} $$

Soit finalement,

$$\overline{OA} \times \hspace{0.05em} \overline{OB} =\hspace{0.05em} \overline{OC} \times \overline{OD}$$

Cas 2 : Point extérieur au cercle

Soit un cercle et deux cordes $AB$ et $CD$ telle que la figure suivante :

Puissance d'un point par rapport à un cercle - point extérieur

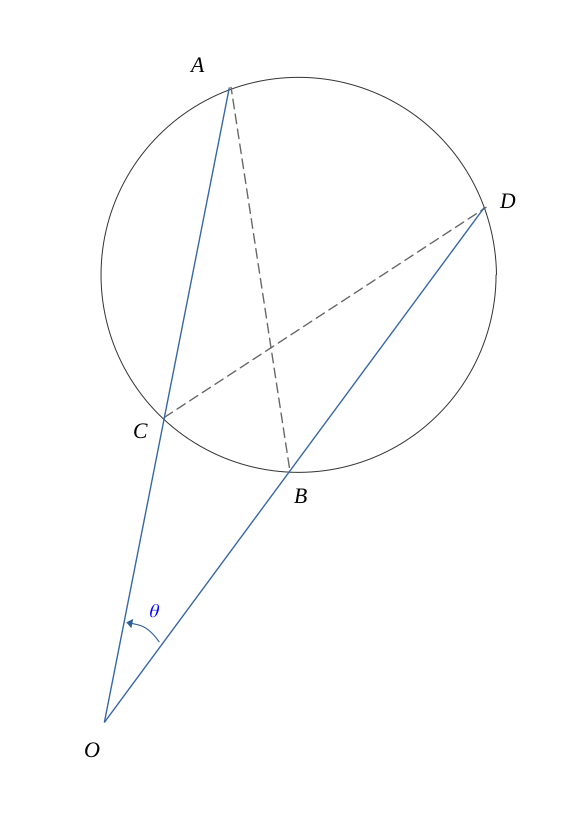
Le point $O$ est le point d'intersection entre les droites $(AC)$ et $(BD)$ à l'extérieur du cercle, cette intersection forme un sommet d'angle $\theta$.

Les angles $ \widehat{BAC}$ et $ \widehat{BDC}$ inteceptent le même arc $ \overset{\frown}{BC}$ sur le cercle. Ils sont donc égaux.

$$ \widehat{BAC} = \widehat{BDC} = \alpha $$

Par suite, les mesures des angles $ \widehat{ABO}$ et $ \widehat{DCO}$ sont égales, étant le troisième angle des deux triangles respectifs :

$$ \widehat{ABO} = \widehat{DCO} = \beta = \pi - (\alpha + \theta) $$

Les deux triangles $ ABO $ et $ DCO $ ayant deux angles deux-à-deux respectivement égaux, ils sont semblables.

On alors les proportions suivantes :

$$ \frac{OA}{OC} = \frac{OD}{OB} $$

Soit finalement,

$$\overline{OA} \times \hspace{0.05em} \overline{OB} =\hspace{0.05em} \overline{OC} \times \overline{OD}$$

Cas 3 : Point extérieur au cercle avec une tangente

En reprenant notre figure précédente en faisant tendre les points $B$ et $D$ vers un nouveau point $T$, pour que la droite $(OT)$ soit tangente au cercle.

Puissance d'un point par rapport à un cercle - point extérieur (construction d'une tangente T)

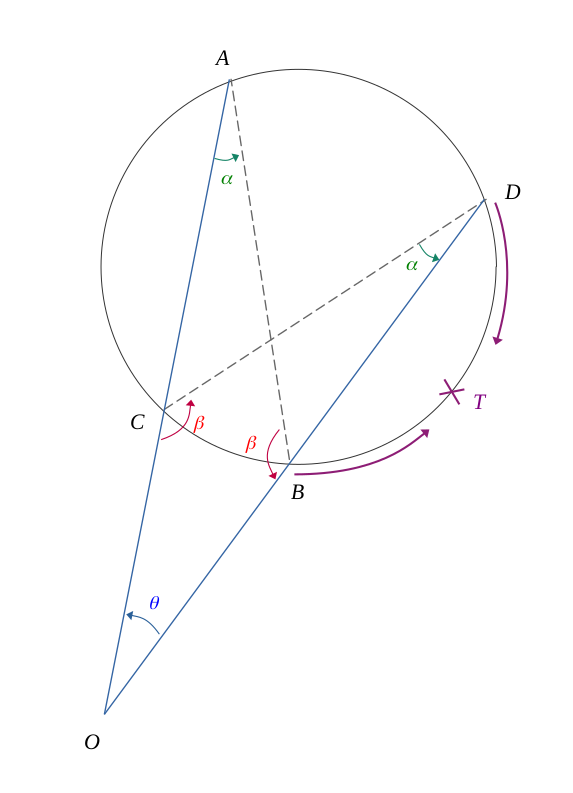
En construisant ce nouveau point $T$, on a conservé l'équivalence entre les deux angles $\alpha$.

Les deux triangles $ OAT $ et $ CTO $ ayant deux angles deux-à-deux respectivement égaux, ils sont semblables.

On alors les proportions suivantes :

$$ \frac{OA}{OT} = \frac{OT}{OC} $$

Soit finalement,

$$\overline{OA} \times \hspace{0.05em} \overline{OC} =\hspace{0.05em} \overline{OT} ^2$$

Cas 4 : Point extérieur au cercle avec deux tangentes

En reprenant notre figure précédente et en faisant tendre cette fois les points $A$ et $C$ vers un nouveau point $T'$, pour que la droite $(OT')$ soit tangente au cercle.

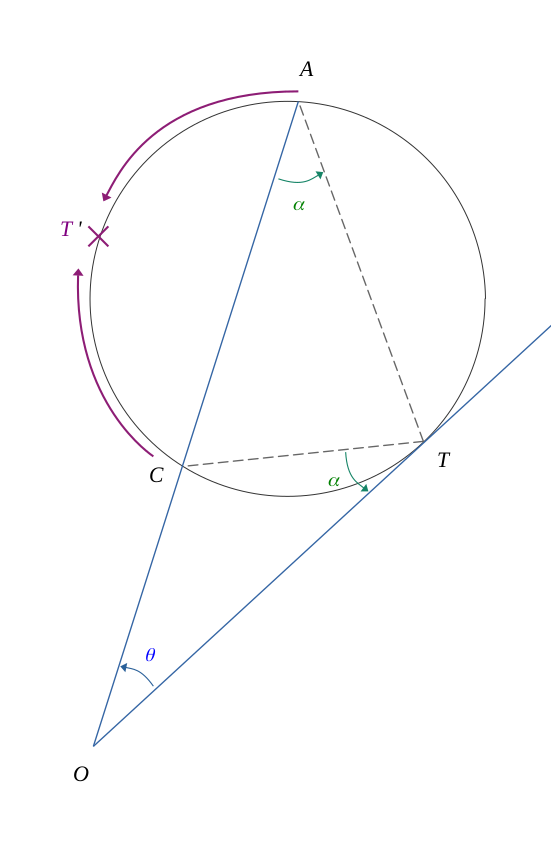
En construisant ce nouveau point $T'$, on a conservé l'équivalence entre les deux angles $\alpha$.

Les deux triangles semblables s'étant confondus lors du glissement, on se retrouve alors avec un seul triangle $OTT'$ isocèle.

Alors,

$$\overline{OT} = \hspace{0.05em} \overline{OT'}$$