







Dans un contexte d'un triangle quelconque \(\{a, b, c\}\), avec chaque angle opposé respectivement à sa longueur, tel que :
$$ \left \{ \begin{gather*} \alpha \enspace opposé \enspace à \enspace a \\ \beta \enspace opposé \enspace à \enspace b \\ \gamma \enspace opposé \enspace à \enspace c \end{gather*} \right \} $$
Et tel que la figure suivante :
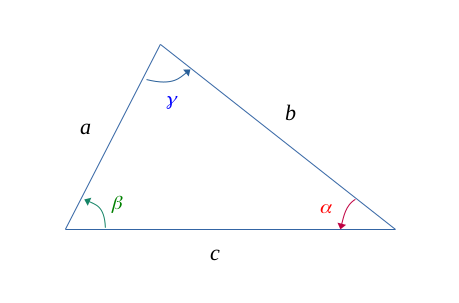
La loi des sinus nous dit que :
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3, \enspace (\alpha, \beta, \gamma) \in \hspace{0.05em} \mathbb{R}^3, $$
$$ \frac{sin(\alpha)}{a} = \frac{sin(\beta)}{b} = \frac{sin(\gamma)}{c} $$
Pour le démontrer, projectons une hauteur \( h_c \) sur la longueur \( c \), et telle que la figure suivante :
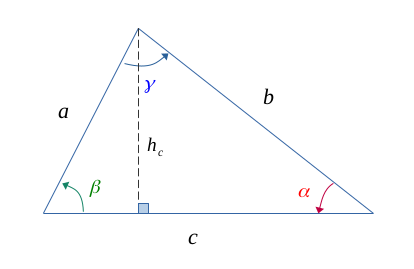
Immédiatement, il vient les relations suivantes :
$$ sin(\alpha) = \frac{h_c}{b} \qquad (1) $$
$$ sin(\beta) = \frac{h_c}{a} \qquad (2) $$
En divisant l'égalité \( (1) \) par \( a \), on a :
$$ \frac{sin(\alpha)}{a} = \frac{h_c}{ab} \qquad (3) $$
De la même manière, on divise \( (2) \) par \( b \) :
$$ \frac{sin(\beta)}{b} = \frac{h_c}{ab} \qquad (4) $$
On voit que les membres de droite de \( (3) \) et \( (4) \) sont équivalents, il s'en suit que :
$$ \frac{sin(\alpha)}{a} = \frac{sin(\beta)}{b} \qquad (5) $$
En reproduisant cette opération sur les deux autres longueurs du triangle, on aura deux nouvelles équations :
$$ \frac{sin(\beta)}{b} = \frac{sin(\gamma)}{c} \qquad (6) $$
$$ \frac{sin(\gamma)}{c} = \frac{sin(\alpha)}{a} \qquad (7) $$
Les égalités \( (5), (6), (7) \) ayant un membre commun deux-à-deux, elles sont toutes les trois égales.
Et finalement,
$$\forall (a, b, c) \in \hspace{0.05em} \mathbb{R}^3, \enspace (\alpha, \beta, \gamma) \in \hspace{0.05em} \mathbb{R}^3, $$
$$ \frac{sin(\alpha)}{a} = \frac{sin(\beta)}{b} = \frac{sin(\gamma)}{c} $$
 Retour en haut de page
Retour en haut de page