Imprimer

Lois géométriques du triangle

Dans un triangle ordinaire

Dans un triangle ordinaire $\bigl \{ a, b, c\bigr\}$ tel que la figure suivante :

Sommes des angles

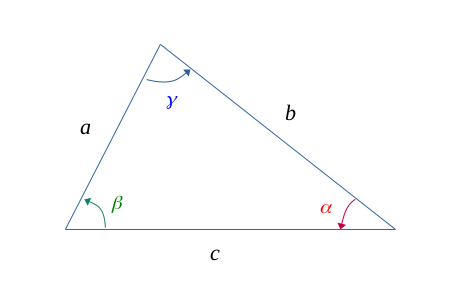
La somme des angles d'un triangle fait toujours $180°$ $(\pi \ radians) $ .

$$ \alpha + \beta + \gamma = 180 \qquad \bigl[deg \bigr] $$

$$ \alpha + \beta + \gamma = \pi \qquad \bigl[rad \bigr] $$

Calcul d'une aire

Avec deux longueurs et un angle partant d'un sommet commun

$$ S = \frac{1}{2}sin(\alpha)b c $$

$$ S = \frac{1}{2}sin(\beta)ac$$

$$ S = \frac{1}{2}sin(\gamma)ab $$

Avec les longueurs uniquement (formule de Héron)

$$ S = \sqrt{p(p-a)(p-b)(p-c)} \qquad (H\textit{é}ron) $$

$$ avec \enspace \Biggl \{ \begin{gather*} p : demi\hspace{-0.3em}-\hspace{-0.3em}p\textit{é}rim\textit{è}tre \ du \ triangle \\ p = \frac{a+b+c}{2} \end{gather*} $$

Théorème d'Al-Kashi

Ce théorème peut être utile pour calculer des longueurs dans un triangle non rectangle.

Si l'angle connu est droit, on retrouve le théorème de Pythagore.

$$ a^2 = b^2 + c^2 - 2bc.cos(\alpha) \qquad (Al-Kashi) $$

$$ b^2 = a^2 + c^2 - 2ac.cos(\beta) \qquad (Al-Kashi^*) $$

$$ c^2 = a^2 + b^2 - 2ab.cos(\gamma) \qquad (Al-Kashi^{**}) $$

Loi des sinus

Cette formule peut être utile pour :

retrouver un côté connaissant un côté et deux angles
retrouver un angle connaissant un angle et deux côtés

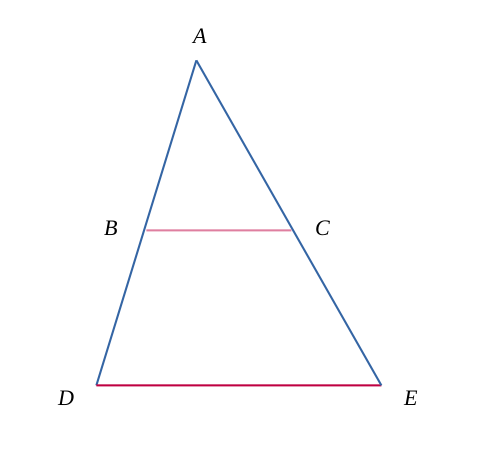
$$ \frac{sin(\alpha)}{a} = \frac{sin(\beta)}{b} = \frac{sin(\gamma)}{c} $$

Théorème de Thalès

Dans deux triangles semblables imbriqués $ ABC $ et $ ADE $, où $ADE$ est le plus grand triangle.

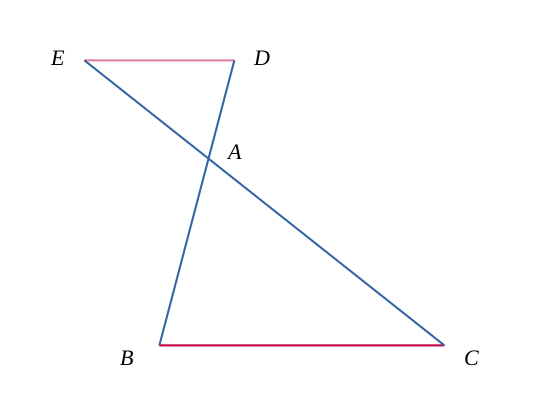
Ou encore dans le cas où les deux triangles sont semblables par l'extérieur (en conservant l'alignement des points précédents).

Deux triangles semblables (imbriqués par l'extérieur)

$$ BC \parallel DE \Longleftrightarrow \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \qquad \bigl(Thal\textit{è}s \bigr) $$

(deux égalités sur trois sont suffisantes)

Ce théorème permet de :

retrouver un côté connaissant les deux autres
prouver que deux longueurs sont parallèles ou non

Dans un triangle rectangle

Dans un triangle rectangle $\bigl \{ a, b, c\bigr\}$ tel que la figure suivante :

Théorème de Pythagore

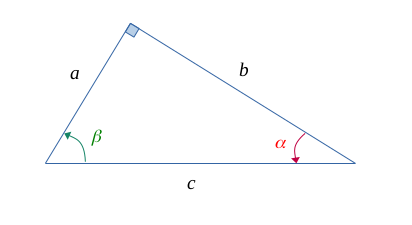
Ce théorème permet de :

retrouver un côté connaissant les deux autres
prouver qu'un angle est rectangle ou non

$$ (a \perp b) \Longleftrightarrow a^2 + b^2 = c^2 \qquad \bigl(Pythagore \bigr) $$

Trigonométrie

Les règles de trigonométrie s'appliquent toujours dans un triangle rectangle.

Un triangle rectangle avec un angle $\alpha$

Relativement à un angle $\alpha$, on a les relations suivantes :

$$sin(\alpha) = \frac{\Bigl[oppos\textit{é}\Bigr]}{\Bigl[hypot\textit{é}nuse\Bigr]}$$

$$cos(\alpha) = \frac{\Bigl[adjacent\Bigr]}{\Bigl[hypot\textit{é}nuse\Bigr]}$$

$$tan(\alpha) = \frac{sin(\alpha)}{cos(\alpha)} = \frac{\Bigl[oppos\textit{é}\Bigr]}{\Bigl[adjacent\Bigr]}$$

Astuce : On peut utiliser le moyen mnémotechnique $SOH-CAH-TOA$.