Imprimer

Vider les graphiques

Actuelle

Autre

Index

Les fonctions trigonométriques de référence

Grâce au théorème de Pythagore, on a toujours la relation fondamentale :

Par ailleurs, les fonctions trigonométriques sont de manière générale des fonctions périodiques.

Fonction sinus : \(f(x) = sin(x)\)

1. Définition

La fonction sinus est définie par :

$$ \forall x \in \hspace{0.03em} \mathbb{R}, $$
$$f(x) = sin(x) $$





Elle est \(2 \pi - \)périodique.

2. Propriétés

$$ \forall x \in \hspace{0.03em} \mathbb{R}, $$

1. Périodicité

$$ \forall k \in \hspace{0.03em} \mathbb{Z}, $$
$$sin(x + 2k \pi) = sin(x)$$

2. En fonction de \(\pi\)

$$sin(\pi + x) = - sin(x)$$
$$sin(\pi - x) = sin(x)$$

3. En fonction de \(\pi \over 2 \)

$$sin\left(\frac{ \pi}{2} + x \right) = cos(x)$$
$$sin\left(\frac{ \pi}{2} - x \right) = cos(x)$$

4. Fonction impaire

$$sin(-x) = - sin(x)$$

5. Linéarisation

$$ \forall \alpha \in \hspace{0.03em} \mathbb{R}, $$
$$sin(2\alpha) = 2sin(\alpha) cos(\alpha)$$

6. Linéarisation par la tangente

$$ \forall \alpha \in \hspace{0.03em} \mathbb{R}, $$
$$sin(2\alpha) = \frac{2tan(\alpha)}{1+tan^2(\alpha)}$$

7. Addition

$$ \forall (\alpha, \beta) \in \hspace{0.03em} \mathbb{R}^2, $$
$$sin(\alpha + \beta) = sin(\alpha) cos(\beta) + sin(\beta) cos(\alpha)$$
$$sin(\alpha \textcolor{#D55454}{-} \beta) = sin(\alpha) cos(\beta) \textcolor{#D55454}{-} sin(\beta) cos(\alpha)$$

Par ailleurs, en posant :

$$ \Biggl \{ \begin{align*} a = \alpha + \beta \\ b = \alpha - \beta \end{align*} $$
$$ sin(a ) + sin(b) = 2 sin\left(\frac{a+b}{2}\right) cos\left(\frac{a-b}{2}\right) $$
$$ sin(a ) - sin(b) = 2 cos\left(\frac{a+b}{2}\right) sin\left(\frac{a-b}{2}\right) $$

Fonction cosinus : \(f(x) = cos(x)\)

1. Définition

La fonction cosinus est définie par :

$$ \forall x \in \hspace{0.03em} \mathbb{R}, $$
$$f(x) = cos(x) $$





Elle est \(2 \pi - \)périodique.

2. Propriétés

$$ \forall x \in \hspace{0.03em} \mathbb{R}, $$

1. Périodicité

$$ \forall k \in \hspace{0.03em} \mathbb{Z}, $$
$$cos(x + 2 k\pi) = cos(x)$$

2. En fonction de \(\pi\)

$$cos(\pi + x) = - cos(x)$$
$$cos(\pi - x) = - cos(x)$$

3. En fonction de \(\pi \over 2\)

$$cos\left(\frac{\pi}{2} + x \right) = - sin(x)$$
$$cos\left(\frac{\pi}{2} - x \right) = sin(x)$$

4. Fonction paire

$$cos(-x) = cos(x)$$

5. Linéarisation

$$ \forall \alpha \in \hspace{0.03em} \mathbb{R}, $$
$$ cos(2\alpha) = cos^2(\alpha) - sin^2(\alpha) $$
$$ cos(2\alpha) = 2cos^2(\alpha) - 1 $$
$$ cos(2\alpha) = 1 - 2sin^2(\alpha) $$

6. Linéarisation par la tangente

$$ \forall \alpha \in \hspace{0.03em} \mathbb{R}, $$
$$ cos(2\alpha) = \frac{1 - tan^2(\alpha)}{1 + tan^2(\alpha)} $$

7. Addition

$$ \forall (\alpha, \beta) \in \hspace{0.03em} \mathbb{R}^2, $$
$$ cos(\alpha + \beta) = cos(\alpha) cos(\beta) - sin(\alpha) sin(\beta)$$
$$ cos(\alpha \textcolor{#D55454}{-} \beta) = cos(\alpha) cos(\beta) \textcolor{#D55454}{+} sin(\alpha) sin(\beta)$$

Par ailleurs, en posant :

$$ \Biggl \{ \begin{align*} a = \alpha + \beta \\ b = \alpha - \beta \end{align*} $$
$$ cos(a ) + cos(b) = 2 cos\left(\frac{a+b}{2}\right) cos\left(\frac{a-b}{2}\right) $$
$$ cos(b ) - cos(a) = 2 sin\left(\frac{a+b}{2}\right) sin\left(\frac{a-b}{2}\right) $$

Fonction tangente : \(f(x) = tan(x)\)

1. Définition

Lorsqu'on représente les sinus et cosinus sur le cercle, on s'aperçoit qu'avec le théorème de Thalès :

$$ \frac{sin(\theta)}{tan(\theta)} = \frac{cos(\theta)}{1} $$


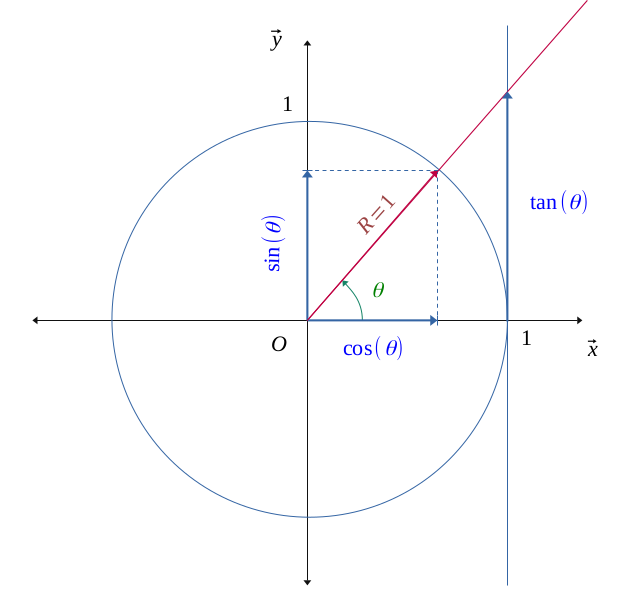
D'où :

$$tan(\theta) = \frac{sin(\theta)}{cos(\theta)} $$

Alors, la fonction tangente est définie par :

$$\forall k \in \mathbb{Z}, \enspace \forall x \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \left\{ \frac{\pi}{2} + k\pi \right\} \Bigr],$$
$$f(x) = tan(x) = \frac{sin(x)}{cos(x)}$$





Cette fonction est \(\pi - \)périodique.

2. Propriétés

$$ \forall x \in \hspace{0.03em} \mathbb{R}, $$

1. Périodicité

$$ \forall k \in \hspace{0.03em} \mathbb{Z}, $$
$$tan(x + k\pi) = tan(x)$$

2. En fonction de \(\pi\)

$$tan(\pi + x) = tan(x)$$
$$cos(\pi - x) = -tan(x)$$

3. En fonction de \(\pi \over 2\)

$$tan\left(\frac{\pi}{2} + x \right) = - \frac{1}{tan(x)}$$
$$tan\left(\frac{\pi}{2} - x \right) = \frac{1}{tan(x)} $$

4. Fonction impaire

$$tan(-x) = -tan(x)$$

5. Linéarisation

$$ \forall k \in \mathbb{Z}, \enspace \forall \alpha \in \Biggl[ \mathbb{R} \hspace{0.2em} \backslash \left\{\frac{\pi}{4} + \frac{k\pi}{2} \right\} \Biggr], $$
$$ tan(2\alpha) = \frac{2tan(\alpha)}{1 -tan^2(\alpha)} $$

6. Addition

$$\forall k \in \mathbb{Z}, \enspace \forall (\alpha, \beta) \in \Bigl[ \mathbb{R} \hspace{0.2em} \backslash \left\{ \frac{\pi}{2} + k\pi \right\} \Bigr]^2,$$
$$ tan(\alpha + \beta) = \frac{tan(\alpha) + tan(\beta)}{ 1 - tan(\alpha)tan(\beta) }$$
$$ tan(\alpha \textcolor{#D55454}{-} \beta) = \frac{tan(\alpha) \textcolor{#D55454}{-} tan(\beta)}{ 1 \textcolor{#D55454}{+} tan(\alpha)tan(\beta) }$$