Géométrie du triangle

Dans un triangle ordinaire

Dans un triangle ordinaire $\bigl \{ a, b, c\bigr\}$ avec :

$$ \left \{ \begin{gather*} \alpha \enspace oppos \textit{é} \enspace \textit{à} \enspace a \\ \beta \enspace oppos\textit{é} \enspace \textit{à} \enspace b \\ \gamma \enspace oppos\textit{é} \enspace \textit{à} \enspace c \end{gather*} \right \} $$

Et tel que la figure suivante :

Sommes des angles

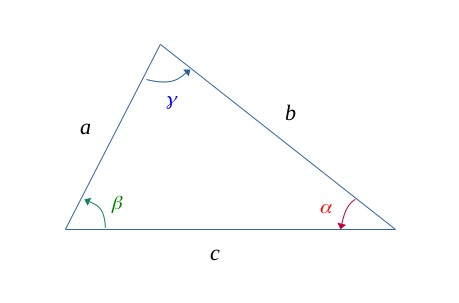
La somme des angles d'un triangle fait toujours $180°$ $(\pi \ radians) $ .

$$ \alpha + \beta + \gamma = 180 \qquad \bigl[deg \bigr] $$

$$ \alpha + \beta + \gamma = \pi \qquad \bigl[rad \bigr] $$

Aire d'un triangle

Dans un triangle ordinaire $ \bigl \{ a,b,c \bigr \}$, pour calculer l'aire du triangle, on projette une hauteur sur un des côtés, par exemple sur $c$ :

Un triangle ordinaire avec sa hauteur (1)

À partir de cela, on fait :

$$ \mathcal{A} = \frac{c \times h_c}{2} $$

Soit,

Un triangle ordinaire avec sa hauteur (2)

$$\mathcal{A} = \frac{base \times hauteur}{2} $$

Similarités de deux triangles

Deux triangles semblables

Deux triangles sont dit semblables lorsqu'ils ont leurs longueurs respectives proportionnelles et leurs angles respectivement égaux.

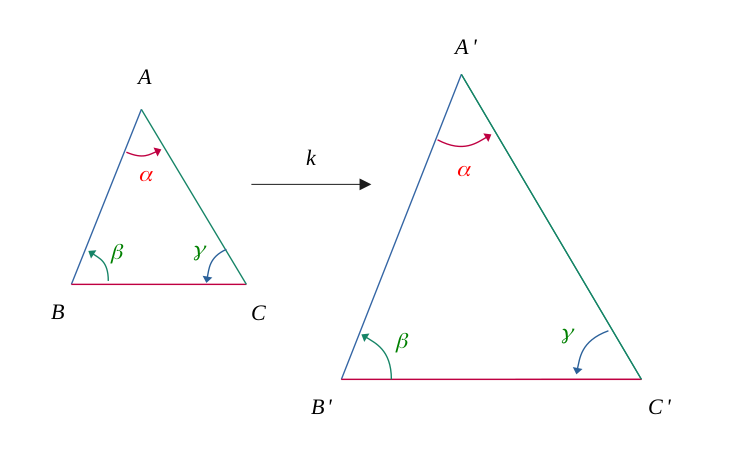
Cela implique alors un rapport $k$ entre les longueurs respectives, correspondant à un agrandissement, une réduction ou une conservation (si $k = 1$).

$$ \exists! k \in \mathbb{R}, \ \begin{Bmatrix} \overline{A'B'} = k \times \overline{AB}\\ \overline{B'C'} = k \times \overline{BC} \\ \overline{A'C'} = k \times \overline{AC} \end{Bmatrix} $$

$$ \begin{Bmatrix} \widehat{BAC} = \widehat{B'A'C'} = \alpha \\ \widehat{ABC} = \widehat{A'B'C'} = \beta \\ \widehat{BCA}= \widehat{B'C'A'} = \gamma \end{Bmatrix} $$

Il existe pricipalement trois cas de similarités de triangles.

Deux triangles sont semblables :

s'ils ont leurs trois côtés respectifs proportionnels.
s'ils ont au moins deux angles deux-à-deux égaux.
s'ils ont un angle commun et qu'ils ont les deux longueurs respectives proportionnelles

Théorème(s) de Thalès

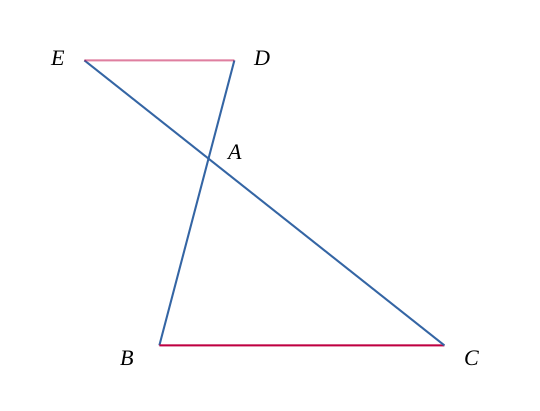
Soit un triangle ordinaire $ADE$, et une droite $BC$ passant respectivement par les côtés $AD$ et $AC$.

Il existe deux configurations où le théorème s'exprime :

La première configuration dans lequel s'applique ce théorème est le cas de deux triangles semblables imbriqués $ ABC $ et $ ADE $, où $ADE$ est le plus grand triangle.

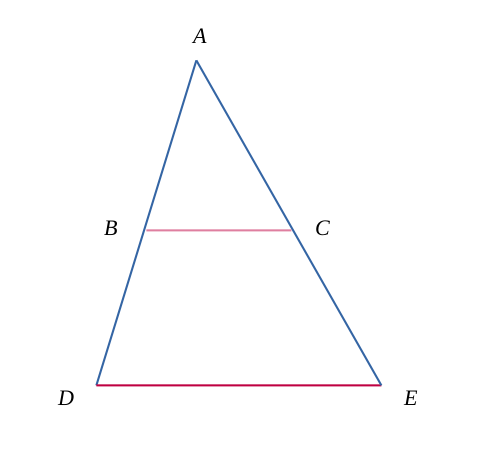
La seconde configuration est le cas où les deux triangles sont semblables mais par l'extérieur (en conservant l'alignement des points précédents), et telle que la figure suivante :

Deux triangles semblables (imbriqués par l'extérieur)

Théorème

Le théorème exprime que s'il existe une relation de parallélisme, alors il existe aussi une relation de proportionnalité entre les longueurs, telle que :

$$(BC) \parallel (DE) \Longrightarrow \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \qquad \bigl(Thal\textit{è}s \enspace(th \textit{é} or \textit{è} me) \bigr) $$

Réciproque

Sa réciproque à l'inverse, permet de déduire une relation de parallélisme à partir de relations de proportionnalité.

$$ \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \Longrightarrow (BC) \parallel (DE) \qquad \bigl(Thal\textit{è}s \enspace(r\textit{é}ciproque) \bigr) $$

Même si dans les faits, seulement deux de ces égalités suffisent à prouver le prallélisme :

$$ \Biggl( \frac{AB}{AD} = \frac{AC}{AE}\Biggr) \ ou \ \Biggl(\frac{AB}{AD} = \frac{BC}{DE} \Biggr) \ ou \ \Biggl(\frac{AC}{AE} = \frac{BC}{DE}\Biggr) \Longrightarrow (BC) \parallel (DE) \qquad \bigl(Thal\textit{è}s \enspace(réciproque^*) \bigr) $$

Équivalence

Comme pour le théorème de Pythagore, l'équivalence issue des deux implications permettent d'établir une liaison forte entre le parallélisme et le rapport de proportionnalité des longueurs semblables.

$$ (BC) \parallel (DE) \Longleftrightarrow \Biggl( \frac{AB}{AD} = \frac{AC}{AE} = \frac{BC}{DE} \Biggr) \qquad \bigl(Thal\textit{è}s \enspace(\textit{é}quivalence) \bigr) $$

L'une et l'autre sont toujours dans le même état logique.

Corollaire du théorème de Thalès

Deux triangles semblables (imbriqués) avec relation de proportionnalité de $\frac{1}{2}$

$$ \Bigl( D \ milieu \ de \bigl[ AB \bigr] \Bigr) \ et \ \Bigl( E \ milieu \ de \bigl[ AC \bigr] \Bigr) \Longleftrightarrow \biggl( (DE) \parallel (BC) \biggr) \ et \ \Biggl( DE = \frac{1}{2}BC \Biggr) \qquad \bigl(Thal\textit{è}s \enspace(corollaire) \bigr) $$

Dans un triangle rectangle

Théorème(s) de Pythagore

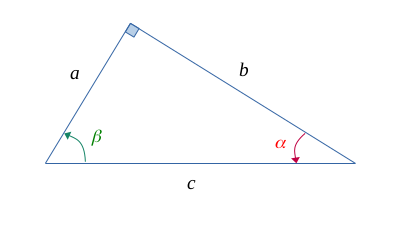
Soit un triangle $ \bigl \{ a,b,c \bigr \}$, où $c$ est le plus grand côté.

Théorème

Le théorème de Pythagore part de l'hypothèse que le triangle est rectangle entre $a$et, $b$ pour en déduire une égalité entre les longueurs du triangle.

$$ (a \perp b )\Longrightarrow a^2 + b^2 = c^2 \qquad \bigl(Pythagore \enspace(th \textit{é} or \textit{è} me) \bigr) $$

Le théorème de Pythagore

Pour prouver la véracité du thèorème, nous avons projeté la hauteur $ h_c$ sur l'hypoténuse $ c$, ce qui divise cette longueur en deux côtés : $m$ et $n$.

Projection de la hauteur sur l'hypoténuse $c$

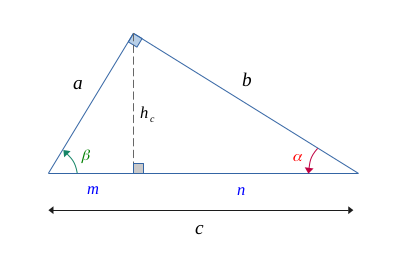
On sait que la somme des angles d'un triangle est égal à $\pi \enspace (180°)$ .

Or, dans le triangle principal formé par $\{a, b, c\}$, on remarque que $\alpha + \beta + \frac{\pi}{2} = \pi$.

Cette relation générale va nous permettre de déduire d'autres angles.

Dans le second triangle formé par $\{m, \; h_c, \; a\}$, on a un angle droit et l'angle $\beta$. Le troisième angle est alors $\alpha$.

Enfin, dans le dernier triangle formé par $\{h_c, \; n, \; b\}$, on a un angle droit et l'angle $\alpha$. Le troisième angle est donc $\beta$.

Nous les avons ajoutés à la figure suivante :

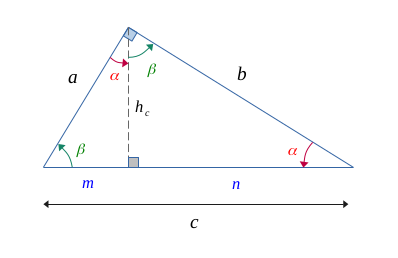
Une propriété des triangles semblables nous dit que lorsque deux triangles ont deux-à-deux les mêmes angles, ils sont semblables, et auront alors deux-à-deux leurs côtés similaires formant un même ratio.

Dans ce cas, on a les relations suivantes :

$$ \frac{a}{c} = \frac{m}{a} = \frac{h_c}{b} $$

$$ \frac{a}{c} = \frac{m}{a} \qquad (1)$$

$$ \frac{b}{c} = \frac{n}{b} = \frac{h_c}{a} $$

$$ \frac{b}{c} = \frac{n}{b} \qquad (2)$$

Grâce aux expressions $(1)$ et $(2)$, on a :

$$ \Biggl \{ \begin{gather*} a^2 = cm \qquad (3) \\ b^2 = cn \qquad \ (4) \end{gather*} $$

Maintenant, en additionnant $(3) $ et $(4)$, on obtient :

$$ a^2 + b^2 = cm + cn$$

$$ a^2 + b^2 = c(m + n) $$

Mais $ (m + n = c) $, soit finalement :

$$ a \perp b \Longrightarrow a^2 + b^2 = c^2 \qquad \bigl(Pythagore \enspace(th \textit{é} or \textit{è} me) \bigr) $$

Réciproque

La réciproque du théorème part de l'hypothèse de l'existance de cette égalité entre les longueurs, pour en déduire le caractère rectangle du triangle.

$$ a^2 + b^2 = c^2 \Longrightarrow (a \perp b) \qquad \bigl(Pythagore \enspace(r\textit{é}ciproque) \bigr) $$

Équivalence

Comme précédemment pour le théorème de Thalès, l'un et l'autre forment une équivalence.

$$ (a \perp b) \Longleftrightarrow a^2 + b^2 = c^2 \qquad \bigl(Pythagore \enspace( \textit{é} quivalence) \bigr) $$

Triangle de proportions $(3 \ / \ 4 \ / \ 5)$

Soit un $ k \in \hspace{0.03em} \mathbb{R}^+ $ un réel positif, et un triangle de longueurs respectives $ \Bigl \{ a = 3k, \ b = 4k, \ c = 5k \Bigr \} $.

Tout triangle de proportions $(3 \ / \ 4 \ / \ 5)$ est un triangle rectangle

Soit un $ k \in \hspace{0.03em} \mathbb{R}^+ $ un réel positif, et un triangle de longueurs respectives $ \Bigl \{ a = 3k, \ b = 4k, \ c = 5k \Bigr \} $.

On essaye de vérifier si ce triangle est rectangle, on calcule alors :

$$a^2 + b^2 = (3k)^2 + (4k)^2 $$

$$a^2 + b^2 = 9k^2 + 16k^2 $$

$$a^2 + b^2 = 25k^2 $$

$$ c^2 = (5k)^2 $$

$$ c^2 = 25k^2 $$

On a bien :

$$ \forall k \in \mathbb{R}, \ a^2 + b^2 = c^2 $$

Donc si l'on applique la réciproque du théorème de Pythagore, on a :

$$ a^2 + b^2 = c^2 \Longrightarrow (a \perp b) \qquad \bigl(Pythagore \enspace(r\textit{é}ciproque) \bigr) $$

Donc le triangle est bien rectangle entre $a$ et $b$.

Trigonométrie

Les règles de trigonométrie s'appliquent toujours dans un triangle rectangle.

Un triangle rectangle avec un angle $\alpha$

Relativement à un angle $\alpha$, on a les relations suivantes :

$$\forall \alpha \in \mathbb{R}, $$

$$sin(\alpha) = \frac{\Bigl[oppos\textit{é}\Bigr]}{\Bigl[hypot\textit{é}nuse\Bigr]}$$

$$cos(\alpha) = \frac{\Bigl[adjacent\Bigr]}{\Bigl[hypot\textit{é}nuse\Bigr]}$$

$$tan(\alpha) = \frac{sin(\alpha)}{cos(\alpha)} = \frac{\Bigl[oppos\textit{é}\Bigr]}{\Bigl[adjacent\Bigr]}$$

Astuce : On peut utiliser le moyen mnémotechnique $SOH-CAH-TOA$.

$$sin(\alpha) = \frac{\Bigl[O\Bigr]}{\Bigl[H\Bigr]}$$

$$cos(\alpha) = \frac{\Bigl[A\Bigr]}{\Bigl[H\Bigr]}$$

$$tan(\alpha) = \frac{\Bigl[O\Bigr]}{\Bigl[A\Bigr]}$$

Exemple :

Dans le triangle rectangle suivant :

On aura les relations suivantes :

$$\forall \alpha \in \mathbb{R}, $$

$$sin(\alpha) = \frac{a}{c}$$

$$cos(\alpha) = \frac{b}{c}$$

$$tan(\alpha) = \frac{b}{a}$$