Imprimer

Vider les textes à trous

Actuelle

Autre

Index

Géométrie du cercle

Aire d'un disque

Soit un cercle de rayon \(R\).

1. Disque entier

L'aire du disque entier est :

$$S_{2\pi} = \pi R^2$$

2. Disque partiel



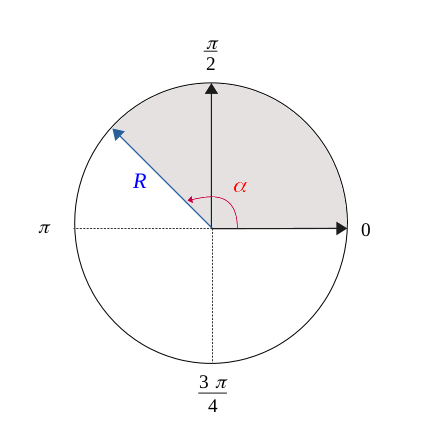
L'aire du disque partiel rempli par un angle \(alpha\) est :

$$S_{\alpha} = \frac{\alpha}{2} R^2$$

Trigonométrie

1. Définition

La trigonométrie s'effectue dans un cercle de rayon \((R = 1) \). On appelle \(\theta\) l'angle formé au centre du cercle dans le sens anti-horaire.

On a :

• \(cos(\theta)\) : la valeur lue sur l'axe horizontal \(\vec{x}\) du projeté orthogonal du rayon \(R\)

• \(sin(\theta)\) : la valeur lue sur l'axe vertical \(\vec{y}\) du projeté orthogonal du rayon \(R\)

• \(tan(\theta)\) : la longueur entre horizontal \(\vec{x}\) et l'intersection de la tangente au cercle et la prolongation de rayon \(R\)



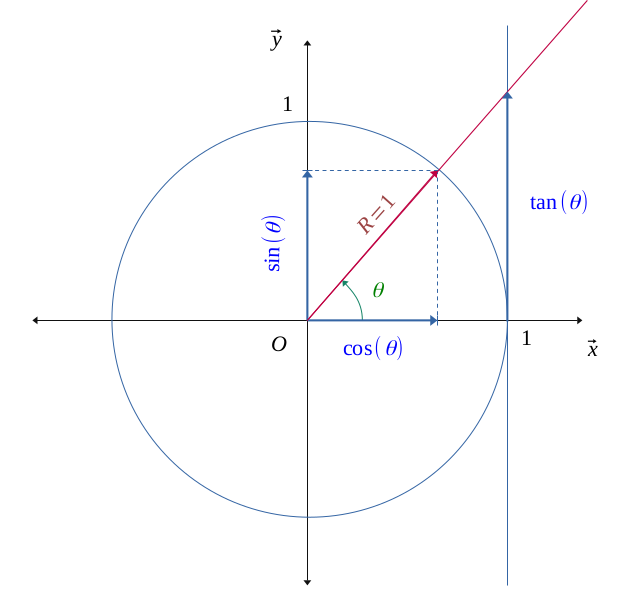
Grâce au théorème de Thalès, on peut voir les relations suivantes :

$$ \frac{cos(\theta)}{1} = \frac{sin(\theta)}{tan(\theta)} $$

Ce qui nous donne la relation :

$$\forall \theta \in \mathbb{R},$$
$$ tan(\theta) = \frac{sin(\theta)}{cos(\theta)} $$

2. Relation fondamentale




De plus, grâce au théorème de Pythagore, on a toujours la relation fondamentale :

$$\forall \theta \in \mathbb{R}, $$
$$cos^2(\theta) + sin^2(\theta) = 1 $$


3. Valeur remarquables



$$ \left \{ \begin{gather*} cos \left( \frac{\pi}{6} \right) = \frac{\sqrt{3}}{2} \\ sin \left( \frac{\pi}{6} \right) = \frac{1}{2} \end{gather*} \right \} $$



$$ \left \{ \begin{gather*} cos \left( \frac{\pi}{4} \right) = \frac{\sqrt{2}}{2} \\ sin \left( \frac{\pi}{4} \right) = \frac{\sqrt{2}}{2} \end{gather*} \right \} $$



$$ \left \{ \begin{gather*} cos \left( \frac{\pi}{3} \right) = \frac{1}{2} \\ sin \left( \frac{\pi}{3} \right) = \frac{\sqrt{3}}{2} \end{gather*} \right \} $$

4. Formules de trigonométrie

$$ \forall \theta \in \mathbb{R}, $$

1. Périodicité

$$ \forall k \in \hspace{0.03em} \mathbb{Z}, $$
$$sin(\theta + 2k \pi) = sin(\theta)$$
$$cos(\theta + 2 k\pi) = cos(\theta)$$

2. En fonction de \(\pi\)

$$sin(\pi + \theta) = - sin(\theta)$$
$$sin(\pi - \theta) = sin(\theta)$$
$$cos(\pi + \theta) = - cos(\theta)$$
$$cos(\pi - \theta) = - cos(\theta)$$

3. En fonction de \(\pi \over 2 \)

$$sin\left(\frac{ \pi}{2} + \theta \right) = cos(\theta)$$
$$sin\left(\frac{ \pi}{2} - \theta \right) = cos(\theta)$$
$$cos\left(\frac{\pi}{2} + \theta \right) = - sin(\theta)$$
$$cos\left(\frac{\pi}{2} - \theta \right) = sin(\theta)$$

4. Parité

La fonction \(sin(\theta) \) est une fonction impaire, donc :

$$sin(-\theta) = - sin(\theta)$$

La fonction \(cos(\theta) \) est une fonction paire, donc :

$$cos(-\theta) = cos(\theta)$$

Théorèmes divers

1. Triangle inscrit dans un cercle

Soit un triangle \(ABC\) inscrit dans un cercle, avec \(BC\) comme plus grand côté.

Si ce plus grand côté \(BC\) est le diamètre du cercle, alors ce triangle \(ABC\) est un triangle rectangle en \(A\).



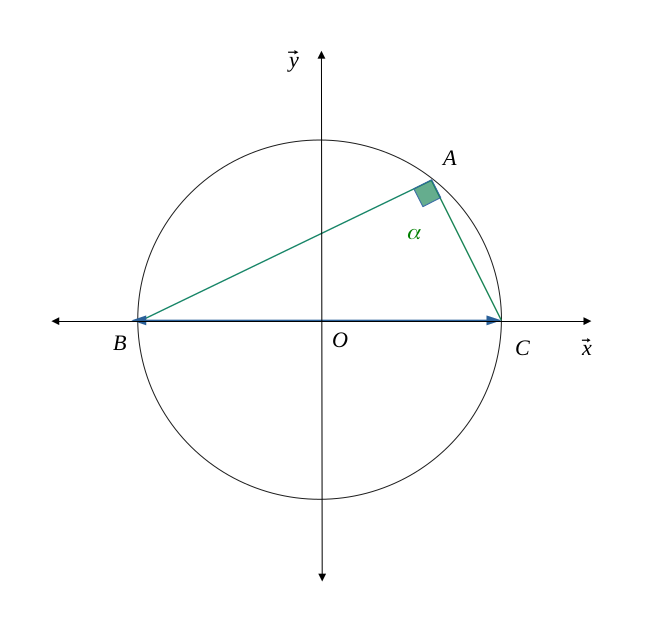
Dans un cercle, si un triangle inscrit a pour plus grand côté le diamètre de ce cercle, alors ce triangle est rectangle.

2. Angle interceptant le même arc que l'angle au centre

Soit un triangle \(ABC\) inscrit dans un cercle, et un autre tiangle \(BOC\), passant par \(O\), le centre du cercle.



Les deux triangles \(ABC\) et \(BOC\) interceptant le même arc \(\overset{\frown}{BC}\), et :

$$ \Biggl \{ \begin{gather*} \alpha = \widehat{BAC} \\ \alpha' = \widehat{BOC} \end{gather*} $$

Dans ce contexte, on a alors :

$$\alpha' = 2 \alpha$$

Soit,

Dans un cercle, la mesure de l'angle inscrit dans un cercle vaut la moitie de l'angle inscrit au centre, et interceptant le même arc.