Imprimer

Méthodes de calculs topologiques

Calculer une pente

Une pente

La pente, souvent exprimée en $\%$, est le ratio entre le dénivelé et la distance horizontale que l'on aura parcouru en se baladant d'un point $A$ à un point $B$ le long d'un chemin pentu.

$$ Pente \ [\%] = \frac{hauteur}{distance} \times 100 $$

Attention, ici la pente est bien exprimée en pourcentage.

Lorsqu'on va au ski, on voit souvent un panneau pour nous dire qu'il y a une pente à $10 \%$. Cela correspond à parcourir un dénivelé de $10$ mètres tous les $100$ mètres.

pente à $10 \%$ correspondante au panneau

Si une pente est à $100 \%$, c'est qu'il y a égalité entre dénivelé et distance, et que l'angle est de $45 \%$.

$$ \Bigl[ Pente = 100 \% \Bigr] \Longleftrightarrow \Bigl[ hauteur = distance \Bigr] $$

Calcul d'une pente avec deux points

Tout comme pour tracer une droite, pour calculer une pente il suffit de deux points.

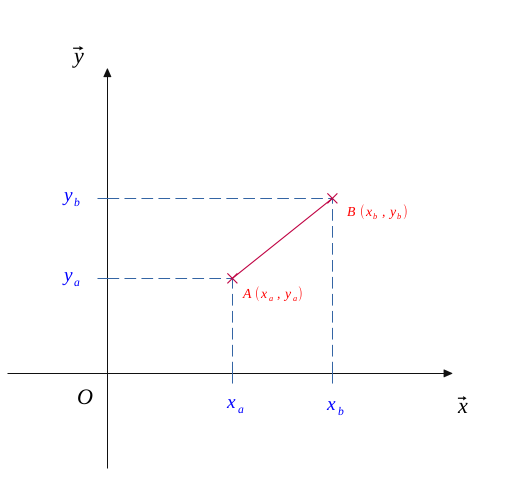
On a représenté sur la figure suivante deux points $A$ et $B$ :

calcul d'une pente à l'aide de deux points $A$ et $B$

Dans notre cas, on calcule la pente grâce à deux points $A(x_a; y_a)$ et $B(x_b; y_b)$ par :

$$ Pente \ [\%] = \frac{ \Bigl[ hauteur(A, B)\Bigr]}{\Bigl[ distance (A, B)\Bigr]} \times 100 $$

$$ Pente \ [\%] = \frac{\Delta y}{\Delta x} \times 100 $$

$$ Pente \ [\%] = \frac{y_b - y_a}{x_b - x_a} \times 100 $$

Se répérer dans l'espace

Soit deux points dans l'espace $A(x_a, y_a, z_a)$ et $B(x_b, y_b, z_b)$.

En deux dimensions

Calculer les coordonnées du vecteur $\overrightarrow{AB}$

$$ \overrightarrow{AB} \ = \begin{pmatrix} x_b-x_a\\ y_b-y_a \end{pmatrix} $$

Calculer la longueur $AB$

$$ AB = \sqrt{(x_b - x_a)^2 + (y_b - y_a)^2 } $$

En trois dimensions

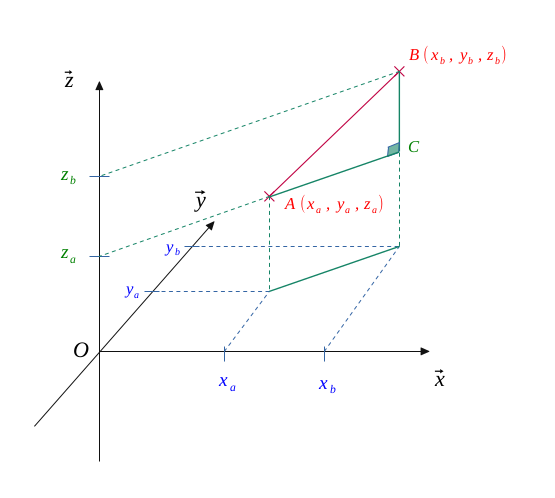
Calculer les coordonnées du vecteur $\overrightarrow{AB}$

$$ \overrightarrow{AB} \ = \begin{pmatrix} x_b-x_a \\ y_b-y_a \\ z_b-z_a \end{pmatrix} $$

Calculer la longueur $AB$

$$ AB = \sqrt{(x_b - x_a)^2 + (y_b - y_a)^2 + (z_b - z_a)^2} $$

Parallélisme / Perpendicularité

Outre les réciproques des théorèmes de Pythagore et Thalès, on peut, en connaissant les coordonnées de deux vecteurs $\overrightarrow{u} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $ et $\overrightarrow{v} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $ :

Vérifier que deux droites sont perpendiculaires

Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ perpendiculaires

Si deux vecteurs sont perpendiculaires, alors leur produit scalaire $(\vec{u} . \vec{v})$ est nul :

$$ \vec{u} \perp \vec{v} \Longleftrightarrow \vec{u}. \vec{v} = 0 $$

$$ \Longleftrightarrow \ x_1 x_2 + y_1 y_2 + z_1 z_2 = 0 $$

Vérifier que deux droites sont parallèles

Deux vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ parallèles

Si deux vecteurs sont parallèles (ou colinéaires), alors leurs coordonnées ont un certain rapport de proportionnalité $k$ (à déterminer) sur les trois dimensions :

$$ \vec{u} \parallel \vec{v} \Longleftrightarrow \vec{u} \hspace{0.03em} = k \times \vec{v}$$

$$ \Longleftrightarrow \ \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \hspace{0.03em} = k \times \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $$

$$ \Longleftrightarrow \ \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \hspace{0.03em} = \begin{pmatrix} k \times x_2 \\ k \times y_2 \\ k \times z_2 \end{pmatrix} $$

De même, on peut aussi vérifier le parallélisme en vérifiant que le produit vectoriel $(\vec{u} \land \vec{v})$ est nul :

$$ \vec{u} \parallel \vec{v} \Longleftrightarrow \vec{u} \land \vec{v} = \vec{0} $$

$$ \Longleftrightarrow \ \begin{pmatrix} y_1 z_2 - y_2 z_1 \\ x_2 z_1- x_1 z_2 \\ x_1 y_2 - x_2 y_1 \end{pmatrix} \hspace{0.03em} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$